题目内容
1.在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.3,-(-1),-1.5,0,-|-2|,-3$\frac{1}{2}$;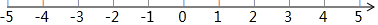
按照从小到大的顺序排列为-3$\frac{1}{2}$<-|-2|<-1.5<0<-(-1).
分析 先在数轴上表示各个数,再比较即可.
解答 解:如图所示: ,
,
则-3$\frac{1}{2}$<-|-2|<-1.5<0<-(-1).
故答案是:-3$\frac{1}{2}$<-|-2|<-1.5<0<-(-1).
点评 本题考查了数轴,有理数的大小比较的应用,能熟记有理数的大小比较法则是解此题的关键,注意:在数轴上表示的数,右边的数总比左边的数大.

练习册系列答案
相关题目
11. 如图,数轴上A,B两点分别对应有理数a,b,则下列结论正确的是( )
如图,数轴上A,B两点分别对应有理数a,b,则下列结论正确的是( )
 如图,数轴上A,B两点分别对应有理数a,b,则下列结论正确的是( )
如图,数轴上A,B两点分别对应有理数a,b,则下列结论正确的是( )| A. | a+b>0 | B. | ab<0 | C. | a-b<0 | D. | b-a>0 |
13.有一种记分法:80分以上如88分记做+8分,某同学得分74分,则应记作( )
| A. | +74分 | B. | +6分 | C. | -6分 | D. | -14分 |
10.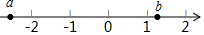 有理数a,b在数轴上的位置如图所示,则下列结论中,不正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,不正确的是( )
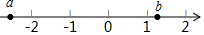 有理数a,b在数轴上的位置如图所示,则下列结论中,不正确的是( )
有理数a,b在数轴上的位置如图所示,则下列结论中,不正确的是( )| A. | a+b<0 | B. | a-b>0 | C. | $\frac{b}{a}$<0 | D. | |a|>|b| |
11. 我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
 我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )
我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图(1)可以用来解释(a+b)2-(a-b)2=4ab.那么通过图(2)面积的计算,验证了一个恒等式,此等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)2=a2+2ab+b2 | D. | (a-b)(a+2b)=a2+ab-2b2 |
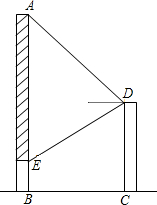 如图,为响应泰安市人民政府“形象重于生命”的号召,在甲建筑物上从A点到E点挂一长为30米的宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,求底部不能直接到达的甲乙两建筑物之间的水平距离BC.
如图,为响应泰安市人民政府“形象重于生命”的号召,在甲建筑物上从A点到E点挂一长为30米的宣传条幅(如图),在乙建筑物的顶部D点测得条幅顶端A点的仰角为45°,测得条幅底端E点的俯角为30°,求底部不能直接到达的甲乙两建筑物之间的水平距离BC.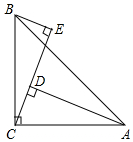 如图,AC=BC,∠ACB=90°,BE⊥CE垂足为E,AD⊥CE垂足为D,AD=5,DE=3,求BE的长.
如图,AC=BC,∠ACB=90°,BE⊥CE垂足为E,AD⊥CE垂足为D,AD=5,DE=3,求BE的长.