题目内容
17.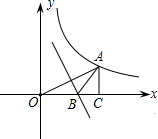 如图,已知点A在双曲线上y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于点C,OA的垂直平分线交OC于点B,△ABC的周长为2$\sqrt{7}$.
如图,已知点A在双曲线上y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于点C,OA的垂直平分线交OC于点B,△ABC的周长为2$\sqrt{7}$.
分析 由双曲线解析式可知,OC×AC=6,由勾股定理可知OC2+AC2=OA2=42,由此可求OC+AC,由垂直平分线的性质可知AB=BO,则AB+BC+AC=AC+BC+BO=AC+CO,即可得出答案.
解答 解:∵点A在双曲线y=$\frac{6}{x}$上,
∴OC×AC=6,
又∵在Rt△ACO中,OC2+AC2=OA2=42,
∴(OC+AC)2=OC2+AC2+2OC×AC=16+12=28,
∴OC+AC=2$\sqrt{7}$,
∵OA的垂直平分线交x轴于点C,
∴AB=BO,
∴AC+BC+AB=AC+BC+BO=AC+OC=2$\sqrt{7}$.
故答案为:2$\sqrt{7}$.
点评 本题考查了反比例函数的综合运用.关键是得到双曲线解析式与相关线段的关系,勾股定理,通过代数式的变形求AC+CO的值.

练习册系列答案
相关题目
7.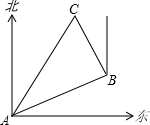 如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )
如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )
 如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )
如图,在一次夏令营活动中,小明从营地A到C地去,先沿北偏东70°方向到达B地,再沿北偏西20°方向到达C地,此时∠ACB=60°,问小明在营地A的( )| A. | 北偏东20°方向上 | B. | 北偏东30°方向上 | C. | 北偏西30°方向上 | D. | 北偏东40°方向上 |
7.某地为了缓解旱情进行了一场人工降雨,现测得6个面积相等区域的降雨量如下表所示:
则这6个区域降雨量的众数和平均数分别为( )
| 区域 | 1 | 2 | 3 | 4 | 5 | 6 |
| 降雨量(mm) | 14 | 12 | 13 | 13 | 17 | 15 |
| A. | 13,13.8 | B. | 14,15 | C. | 13,14 | D. | 14,14.5 |
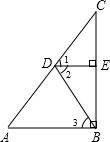 如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据)
如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.(请为每一步推理注明依据)  如图:直线AB,CD相交于点O,EO⊥AB,垂足为O,OF平分∠BOD,∠BOF=15°,求∠COE的度数.
如图:直线AB,CD相交于点O,EO⊥AB,垂足为O,OF平分∠BOD,∠BOF=15°,求∠COE的度数.



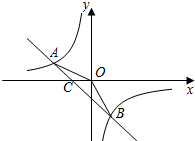 如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.