题目内容
6.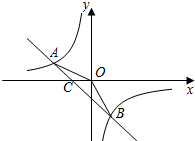 如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,在平面直角坐标系xOy中,若点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标;
(3)求点O到直线AB的距离.
分析 (1)将B坐标代入反比例函数解析式求出m的值,确定出反比例解析式,将A坐标代入反比例解析式求出n的值,确定出A的坐标,将A与B坐标代入一次函数解析式求出k与b的值,即可确定出一次函数解析式;
(2)对于y=-x-1,令y=0求出x的值,即可得出C的坐标;
(3)确定出OC、AB的长,然后根据三角形AOB面积=三角形AOC面积+三角形BOC面积,即可求出.
解答  解:(1)∵点B(1,-2)在函数y=$\frac{m}{x}$的图象上,
解:(1)∵点B(1,-2)在函数y=$\frac{m}{x}$的图象上,
∴m=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$,
∵点A(-2,n)在函数y=-$\frac{2}{x}$的图象上,
∴n=1,即A(-2,1),
∵y=kx+b经过A(-2,1)、B(1,-2),
∴$\left\{\begin{array}{l}{-2k+b=1}\\{k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
∴一次函数的解析式为y=-x-1;
(2)在一次函数的解析式y=-x-1中,令Y=0得x=-1,
∴点C(-1,0),
(3)∵A(-2,1),B(1,-2),C(-1,0),
∴AB=$\sqrt{(-2-1)^{2}+(1+2)^{2}}$=3$\sqrt{2}$,OC=1,
则S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=$\frac{3}{2}$.
设点O到直线AB的距离为d,
∴S△AOB=$\frac{1}{2}$AB•d=$\frac{1}{2}$×$3\sqrt{2}$×d=$\frac{3}{2}$,
∴d=$\frac{\sqrt{2}}{2}$.
∴点O到直线AB的距离为$\frac{\sqrt{2}}{2}$.
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:坐标与图形性质,直线与坐标轴的交点,待定系数法求函数解析式,熟练掌握待定系数法是解本题的关键.

| A. | (1,2) | B. | (5,3) | C. | (2,9) | D. | (-9,-4) |
| A. | $\sqrt{a}$ | B. | $\sqrt{-a}$ | C. | -$\sqrt{a}$ | D. | -$\sqrt{-a}$ |
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{3}$ | C. | $\sqrt{9}$ | D. | $\sqrt{12}$ |
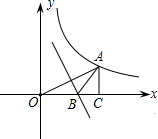 如图,已知点A在双曲线上y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于点C,OA的垂直平分线交OC于点B,△ABC的周长为2$\sqrt{7}$.
如图,已知点A在双曲线上y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于点C,OA的垂直平分线交OC于点B,△ABC的周长为2$\sqrt{7}$.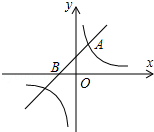 如图,一次函数y=x+1的图象与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2).
如图,一次函数y=x+1的图象与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2).