题目内容
9.在?ABCD中,AB=3,AD=5,AC=4,则?ABCD的面积为12.分析 由AB=3,BC=5,AC=4,即可判定△ABC是直角三角形,则可得AC是高,继而求得?ABCD的面积.
解答 解:如图所示: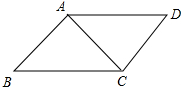
∵四边形ABCD是平行四边形,
∴AD=BC=5,
∵AB=3,AC=4,
∴AB2+AC2=BC2,
∴∠BAC=90°,
即AC⊥AB,
∴S?ABCD=AB•AC=3×4=12.
故答案为:12.
点评 此题考查了平行四边形的性质以及勾股定理的逆定理;证得△ABC是直角三角形是解决问题的关键.

练习册系列答案
相关题目
19.一个正数的算术根为m,则比这个数大2的数的算术平方根是( )
| A. | $\sqrt{{m}^{2}+2}$ | B. | $\sqrt{m+2}$ | C. | m2+2 | D. | m+2 |
20.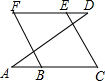 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )
 如图,能够判断FB∥CE的条件是( )
如图,能够判断FB∥CE的条件是( )| A. | ∠F+∠C=180° | B. | ∠ABF=∠C | C. | ∠F=∠C | D. | ∠A=∠D |
4.下列计算错误的是( )
| A. | a8÷a4=a4 | B. | (-a)5÷(-a)4=-a | C. | (-a)5÷(-a4)=a | D. | (b-a)3÷(a-b)2=a-b |
1.某同学利用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出的部分数据如表:
经检查,发现表格中恰好有一组数据计算错误,错误的那组数据的序号是( )
| 序号 | ① | ② | ③ | ④ | ⑤ |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 8 | 3 | 0 | 1 | 0 |
| A. | ① | B. | ② | C. | ③ | D. | ④ |
19. 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
 如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )
如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为弧AB的一个三等分点(靠近点B),D,E分别是OA,OB的中点,则图中阴影部分的面积为( )| A. | $\frac{π+\sqrt{2}-1}{2}$cm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{4π+3\sqrt{3}-3}{6}$cm2 | D. | $\frac{π+\sqrt{3}-1}{2}$cm2 |