题目内容
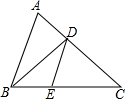 如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求
如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求| S△DCE |
| S 四边形ABED |
考点:相似三角形的判定与性质
专题:
分析:如图,证明△DEC∽△ABC,求出DE的长度,借助相似三角形的性质,即可解决问题.
解答: 解:如图,∵∠B的平分线为BD,DE∥AB,
解:如图,∵∠B的平分线为BD,DE∥AB,
∴∠ABD=∠EBD,∠ABD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE(设为λ);则EC=6-λ;
∵DE∥AB,
∴△DEC∽△ABC,
∴
=
,即
=
,
解得:λ=3.6;设△DEC、△ABC的面积分别为α、β;
∵△DEC∽△ABC,
∴
=(
)2=
,
∴
=
.
即
的值为
.
 解:如图,∵∠B的平分线为BD,DE∥AB,
解:如图,∵∠B的平分线为BD,DE∥AB,∴∠ABD=∠EBD,∠ABD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE(设为λ);则EC=6-λ;
∵DE∥AB,
∴△DEC∽△ABC,
∴
| DE |
| AB |
| EC |
| BC |
| λ |
| 9 |
| 6-λ |
| 6 |
解得:λ=3.6;设△DEC、△ABC的面积分别为α、β;
∵△DEC∽△ABC,
∴
| α |
| β |
| DE |
| AB |
| 4 |
| 25 |
∴
| S△DCE |
| S 四边形ABED |
| 4 |
| 21 |
即
| S△DCE |
| S 四边形ABED |
| 4 |
| 21 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;应牢固掌握相似三角形的判定及其性质,这是灵活解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 四边形ABCD中,AB=BC,BE丄AD垂足为E,∠BCD-∠ABE=90°.过点C作CF∥AD交对角线BD于F,求证:CF=CD.
四边形ABCD中,AB=BC,BE丄AD垂足为E,∠BCD-∠ABE=90°.过点C作CF∥AD交对角线BD于F,求证:CF=CD.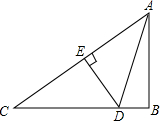 如图,在△ABC中,∠B=90°,斜边AC的垂直平行线交BC于点D,垂足为点E,∠C=40°,求∠BAD的度数.
如图,在△ABC中,∠B=90°,斜边AC的垂直平行线交BC于点D,垂足为点E,∠C=40°,求∠BAD的度数.
 如图,已知AB∥CD,试再添上一个条件,使∠ABF=∠ECD成立.
如图,已知AB∥CD,试再添上一个条件,使∠ABF=∠ECD成立.