题目内容
二次函数y=m(x-
)(x-4)的图象与x轴交于点A、B(点B在点A的右侧),与y轴交于点C.
(1)当m=-1时,求出二次函数图象的顶点坐标;
(2)当△ABC满足以下条件时,分别求出m的值:
①当△ABC的面积为12时;②若△ABC为直角三角形.
| 1 |
| m |
(1)当m=-1时,求出二次函数图象的顶点坐标;
(2)当△ABC满足以下条件时,分别求出m的值:
①当△ABC的面积为12时;②若△ABC为直角三角形.
考点:抛物线与x轴的交点
专题:
分析:(1)求出抛物线的解析式,配成顶点式即可解决问题.
(2)①求出A、B、C三点的坐标,借助面积公式即可解决问题.
②由题意判断m<0,抛物线开口向下,这是解决问题的关键性结论;借助三角形的有关性质求出OA的长,即可解决问题.
(2)①求出A、B、C三点的坐标,借助面积公式即可解决问题.
②由题意判断m<0,抛物线开口向下,这是解决问题的关键性结论;借助三角形的有关性质求出OA的长,即可解决问题.
解答:解:(1)当m=-1时,
y=-x2+3x+4=-(x-1.5)2+
,
故该二次函数图象的顶点坐标为(1.5,6.25).
(2)∵当x=0时,y=4;当y=0时,x=
或4,
∴AB=|4-
|,OC=4;
①∵△ABC的面积为12,
∴
×AB×OC=12,
即
|4-
|×4=12,
解得:m=
或-
.
②由题意可得:当△ABC为直角三角形时,m<0,
抛物线开口向下;
由(2)知:A(
,0)、B(4,0)、C(0,4);
∵△ABC为直角三角形,
∴∠ACB=90°;而OB=OC,
∴∠OCB=∠OBC=45°,
∴∠OAC=∠OCA=45°,
∴OA=OC=4,即-
=4,
解得m=-0.25.
y=-x2+3x+4=-(x-1.5)2+
| 25 |
| 4 |
故该二次函数图象的顶点坐标为(1.5,6.25).
(2)∵当x=0时,y=4;当y=0时,x=
| 1 |
| m |
∴AB=|4-
| 1 |
| m |
①∵△ABC的面积为12,
∴
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| m |
解得:m=
| 1 |
| 10 |
| 1 |
| 2 |
②由题意可得:当△ABC为直角三角形时,m<0,
抛物线开口向下;
由(2)知:A(
| 1 |
| m |
∵△ABC为直角三角形,
∴∠ACB=90°;而OB=OC,
∴∠OCB=∠OBC=45°,
∴∠OAC=∠OCA=45°,
∴OA=OC=4,即-
| 1 |
| m |
解得m=-0.25.
点评:该题主要考查了抛物线与x轴的交点问题;牢固掌握抛物线的性质,灵活运用有关定理来分析、判断是解决抛物线问题的关键;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案
相关题目
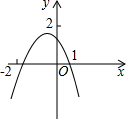 抛物线y=ax2+bx+c的大致图象如图所示,则下列判断正确的有( )个.
抛物线y=ax2+bx+c的大致图象如图所示,则下列判断正确的有( )个.①bc<0;②a+b+c=0;③a<b;④0>a>-2.
| A、1个 | B、2个 | C、3个 | D、4个 |
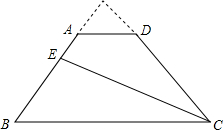 如所示,在梯形ABCD中,AD∥BC,BC=3AD,E是腰AB上的一点,若△BCE和四边形AECD的面积分别为S1和S2,且2S1=3S2,求
如所示,在梯形ABCD中,AD∥BC,BC=3AD,E是腰AB上的一点,若△BCE和四边形AECD的面积分别为S1和S2,且2S1=3S2,求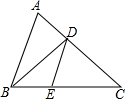 如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求
如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求