题目内容
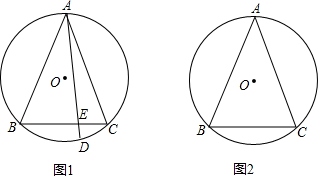
如图,点A、B、C、D在圆O上,且AB=AC.
(1)若D为弧
上一点,如图①,AD交BC于点E.求证:AB2=AD•AE;
(2)若D为弧
上一点,AD交BC的延长线于点E,(1)中的结论还成立吗?请在图②中补出相应图形,并说明理由.
(1)若D为弧
 |
| BC |
(2)若D为弧
 |
| AC |

考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)如图1,作辅助线;证明△ABE∽△ADB,即可解决问题.
(2)如图2,作辅助线;证明△ABE∽△ADB,即可解决问题.
(2)如图2,作辅助线;证明△ABE∽△ADB,即可解决问题.
解答: 证明:(1)如图1,连接BD;
证明:(1)如图1,连接BD;
则∠D=∠C;
∵AB=AC,
∴∠ABC=∠C,
∴∠ABE=∠D;而∠BAE=∠DAB,
∴△ABE∽△ADB,
∴
=
,
∴AB2=AD•AE.
(2)在图2中,结论AB2=AD•AE仍然成立.理由如下:
如图2,连接BD;
则∠ADB=∠ACB;
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABE=∠ADB;
∵∠BAE=∠DAB,
∴△ABE∽△ADB,
∴
=
,
∴AB2=AD•AE.
 证明:(1)如图1,连接BD;
证明:(1)如图1,连接BD;则∠D=∠C;
∵AB=AC,
∴∠ABC=∠C,
∴∠ABE=∠D;而∠BAE=∠DAB,
∴△ABE∽△ADB,
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AD•AE.
(2)在图2中,结论AB2=AD•AE仍然成立.理由如下:
如图2,连接BD;
则∠ADB=∠ACB;
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABE=∠ADB;
∵∠BAE=∠DAB,
∴△ABE∽△ADB,
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AD•AE.
点评:该题以圆为载体,以考查圆周角定理及其推论、相似三角形的判定及其性质等几何知识点为核心构造而成;解题的关键是作辅助线,构造相似三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
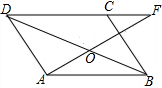 已知,如图,平行四边形ABCD中,F点是DC延长线上的一点,AF交BD于O,交BC于E.求证:
已知,如图,平行四边形ABCD中,F点是DC延长线上的一点,AF交BD于O,交BC于E.求证: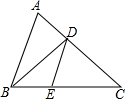 如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求
如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求 一个长方体的左视图,俯视图及相关数据如图所示,求其主视图的面积.
一个长方体的左视图,俯视图及相关数据如图所示,求其主视图的面积.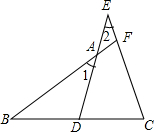 已知,如图,∠1=∠2,BD=CD
已知,如图,∠1=∠2,BD=CD