题目内容
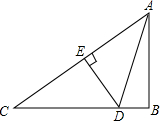 如图,在△ABC中,∠B=90°,斜边AC的垂直平行线交BC于点D,垂足为点E,∠C=40°,求∠BAD的度数.
如图,在△ABC中,∠B=90°,斜边AC的垂直平行线交BC于点D,垂足为点E,∠C=40°,求∠BAD的度数.考点:线段垂直平分线的性质
专题:
分析:先在△ABC中,由∠B=90°,∠C=40°,根据三角形内角和定理求出∠BAC=180°-∠B-∠C=50°.再由DE是AC的垂直平分线,得出AD=CD,根据等边对等角得出∠CAD=∠C=40°,于是∠BAD=∠BAC-∠CAD=50°-40°=10°.
解答:解:在△ABC中,∵∠B=90°,∠C=40°,
∴∠BAC=180°-∠B-∠C=180°-90°-40°=50°.
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠CAD=∠C=40°,
∴∠BAD=∠BAC-∠CAD=50°-40°=10°.
∴∠BAC=180°-∠B-∠C=180°-90°-40°=50°.
∵DE是AC的垂直平分线,
∴AD=CD,
∴∠CAD=∠C=40°,
∴∠BAD=∠BAC-∠CAD=50°-40°=10°.
点评:本题考查了线段垂直平分线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等.也考查了三角形内角和定理和等腰三角形的性质.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
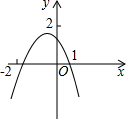 抛物线y=ax2+bx+c的大致图象如图所示,则下列判断正确的有( )个.
抛物线y=ax2+bx+c的大致图象如图所示,则下列判断正确的有( )个.①bc<0;②a+b+c=0;③a<b;④0>a>-2.
| A、1个 | B、2个 | C、3个 | D、4个 |
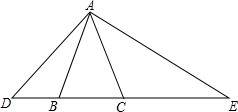 已知,如图,△ABC为等腰三角形,AB=AC,在不添加辅助线的条件下:
已知,如图,△ABC为等腰三角形,AB=AC,在不添加辅助线的条件下: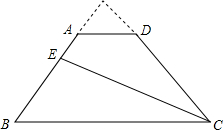 如所示,在梯形ABCD中,AD∥BC,BC=3AD,E是腰AB上的一点,若△BCE和四边形AECD的面积分别为S1和S2,且2S1=3S2,求
如所示,在梯形ABCD中,AD∥BC,BC=3AD,E是腰AB上的一点,若△BCE和四边形AECD的面积分别为S1和S2,且2S1=3S2,求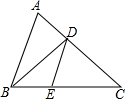 如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求
如图,在△ABC中∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,求