题目内容
2.如图,若点M(m,n)是△ABC内一点,将△ABC平移后得到△DEF,其中点A与点D,点B与点E,点C与点F是对应点,点M (m,n)的对应点M′的坐标是(m+6,n-1)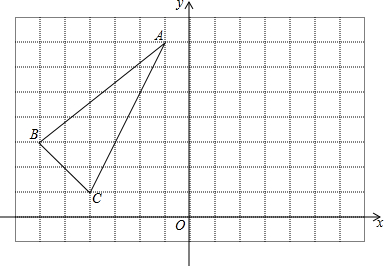
(1)在平面直角坐标系中画出△DEF,并写出点D,点E,点F的坐标;
(2)过点F作FG∥y轴交于DE于点G,求点G的坐标.
分析 (1)根据点M (m,n)的对应点M′的坐标是(m+6,n-1)得出对应点向右平移6个单位,再向下平移1个单位,进而得出答案;
(2)首先求出直线DE的解析式,进而得出G点坐标.
解答  解:(1)如图所示:△DEF即为所求,点D(6,6),点E(0,2),点F(2,0);
解:(1)如图所示:△DEF即为所求,点D(6,6),点E(0,2),点F(2,0);
(2)设直线DE的解析式为:y=kx+b,则$\left\{\begin{array}{l}{6k+b=6}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=2}\end{array}\right.$,
则直线DE的解析式为:y=$\frac{2}{3}$x+2,
当x=2时,y=$\frac{10}{3}$,
故G(2,$\frac{10}{3}$).
点评 此题主要考查了平移变换以及待定系数法求一次函数解析式,得出图形平移规律是解题关键.

练习册系列答案
相关题目
12.直角三角形的三边长是三个连续整数,则各边长分别为( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
13.下列说法正确的是( )
| A. | 两点的所有连线中,直线最短 | |
| B. | 连接两点之间的线段,叫做这两点之间的距离 | |
| C. | 锐角的补角一定是钝角 | |
| D. | 一个角的补角一定大于这个角 |
10.已知⊙O的半径为6cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( )
| A. | 0 | B. | l | C. | 2 | D. | 无法确定 |
 如图,N为函数y=$\frac{3}{x}$图象上一点,NH⊥y轴于点H,则△NOH面积为$\frac{3}{2}$.
如图,N为函数y=$\frac{3}{x}$图象上一点,NH⊥y轴于点H,则△NOH面积为$\frac{3}{2}$.
 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线点F.
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线点F.