题目内容
7.某中学组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
(1)本次随机抽取的学生人数为200人;
(2)求出x值,并将不完整的条形统计图补充完整;
(3)若该校共有学生2500人,试估计每周课外阅读量满足2≤t<4的人数.
分析 (1)由条形图可知A等级有90人,由扇形图可知对应的百分比为45%,那么抽查的学生总数=A等级的人数÷对应的百分比,计算即可求解;
(2)根据所有等级的百分比的和为1,则可计算出x的值,再求出B级与C级的人数,即可作图;
(3)利用每周课外阅读时间量满足2≤t<4的人数=该校总人数×B级的与C级百分比的和计算即可.
解答 解:(1)抽查的学生总数=90÷45%=200人,
(2)∵x%+15%+10%+45%=1,
∴x=30;
B等级的人数=200×30%=60人,
C等级的人数=200×10%=20人,
条形统计图补充如下:
(3)2500×(10%+30%)=1000人,
所以估计每周课外阅读时间量满足2≤t<4的人数为1000人.
故答案为200.
点评 本题主要考查了条形统计图,扇形统计图及用样本估计总体.解题的关键是读懂统计图,能从条形统计图,扇形统计图中得到准确的信息.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18.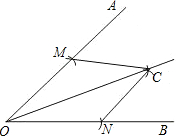 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:
(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于$\frac{1}{2}$MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:(1)以O为圆心,适当长为半径画弧,交OA于点M,交OB于点N.
(2)分别以点M、N为圆心,大于$\frac{1}{2}$MN的长半径画弧,两弧在∠AOB内部相交于点C.
(3)作射线OC.
则判断△OMC≌△ONC的依据是( )
| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
15.在Rt△ABC中,∠C=90°,AC=BC,若以点C为圆心,以2cm长为半径的圆与斜边AB相切,那么BC的长等于( )
| A. | 2cm | B. | 2$\sqrt{2}$cm | C. | 2$\sqrt{3}$cm | D. | 4cm |
19.已知等腰三角形的两条边长分别为2和3,则它的周长为( )
| A. | 7 | B. | 8 | C. | 5 | D. | 7或8 |