题目内容
17. 如图,N为函数y=$\frac{3}{x}$图象上一点,NH⊥y轴于点H,则△NOH面积为$\frac{3}{2}$.
如图,N为函数y=$\frac{3}{x}$图象上一点,NH⊥y轴于点H,则△NOH面积为$\frac{3}{2}$.
分析 设出点N的坐标,根据OH=-y,NH=-x,以及点N在函数y=$\frac{3}{x}$的图象上,结合面积公式求出面积.
解答 解:设N点坐标为(x,y),
∵NH⊥y轴,
∴OH=-y,NH=-x,
∴S△AOB=$\frac{1}{2}$×OB×AB=$\frac{1}{2}$xy,
∵y=$\frac{3}{x}$,
∴xy=3,
∴S△AOB=$\frac{1}{2}$×3=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查的是反比例函数中比例系数k的几何意义,从反比例函数y=$\frac{k}{x}$图象上任意找一点向某一坐标轴引垂线,加上它与原点的连线所构成的直角三角形面积等于|k|的一半.

练习册系列答案
相关题目
9.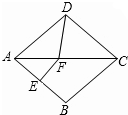 如图,在菱形ABCD中,∠BAD=82°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=82°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
 如图,在菱形ABCD中,∠BAD=82°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )
如图,在菱形ABCD中,∠BAD=82°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于( )| A. | 67° | B. | 57° | C. | 60° | D. | 87° |
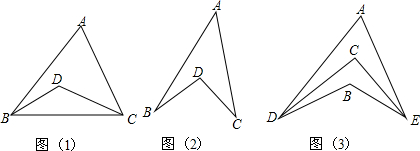
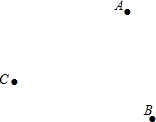 如图,已知点A,B,C不在同一直线上,读下列语句,完成要求:
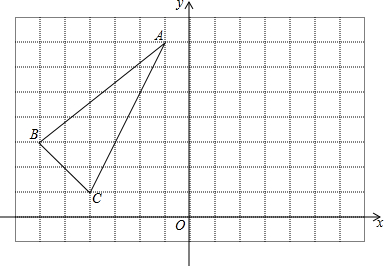
如图,已知点A,B,C不在同一直线上,读下列语句,完成要求: 如图,已知A(0,4),B(-2,-2),C(3,0).
如图,已知A(0,4),B(-2,-2),C(3,0).