题目内容
7.解不等式组:(1)3x-3≤2(2x-1)
(2)$\left\{\begin{array}{l}{2x-1>5}\\{\frac{3x-7}{2}+1≤x}\end{array}\right.$.
分析 (1)去括号,移项,合并同类项,系数化成1即可.
(2)先求出每个不等式的解集,再求出其公共部分即可.
解答 解:(1)3x-3≤2(2x-1),
3x-3≤4x-2,
3x-4x≤-2+3,
-x≤1,
x≥-1.
(2)$\left\{\begin{array}{l}{2x-1>5①}\\{\frac{3x-7}{2}+1≤x②}\end{array}\right.$,
解不等式①得:x>3,
解不等式②得:x≤5,
所以不等式组的解集是:3<x≤5.
点评 本题考查了解一元一次不等式组,熟悉不等式的性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
17.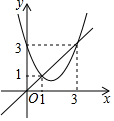 函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
 函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )| A. | 当1<x<3时,x2+(b-1)x+c<0 | B. | b+c=1 | ||
| C. | 3b+c=6 | D. | b2-4c>0 |
15.已知a<b,下列不等式中,变形正确的是( )
| A. | a-3>b-3 | B. | 3a-1>3b-1 | C. | -3a>-3b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
17.正方形的正投影不可能是( )
| A. | 线段 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
 如图,正方形CEFG的顶点E在?ABCD的AD边上,若∠1=35°,∠2=15°,则∠B的度
如图,正方形CEFG的顶点E在?ABCD的AD边上,若∠1=35°,∠2=15°,则∠B的度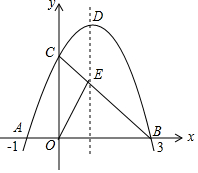 如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.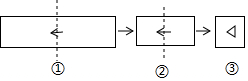 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )
把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )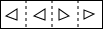
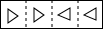
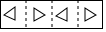

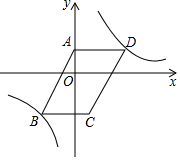 如图,在平面直角坐标系xOy中,双曲线y=$\frac{k}{x}$经过?ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S?ABCD=5.
如图,在平面直角坐标系xOy中,双曲线y=$\frac{k}{x}$经过?ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S?ABCD=5.