题目内容
12.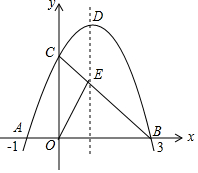 如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.(1)求此抛物线的解析式;
(2)直接写出点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.
注:二次函数y=ax2+bx+c(a≠0)的顶点坐标为(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)
分析 (1)将A、B的坐标代入抛物线的解析式中,即可求出待定系数b、c的值,进而可得到抛物线的对称轴方程;
(2)令x=0,可得C点坐标,将函数解析式配方即得抛物线的顶点C的坐标;
(3)设P(x,y)(x>0,y>0),根据题意列出方程即可求得y,即得D点坐标.
解答 解:(1)由点A(-1,0)和点B(3,0)得$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3;
(2)令x=0,则y=3,
∴C(0,3),
∵y=-x2+2x+3=-(x-1)2+4,
∴D(1,4);
(3)设P(x,y)(x>0,y>0),
S△COE=$\frac{1}{2}$×1×3=$\frac{3}{2}$,S△ABP=$\frac{1}{2}$×4y=2y,
∵S△ABP=4S△COE,∴2y=4×$\frac{3}{2}$,
∴y=3,∴-x2+2x+3=3,
解得:x1=0(不合题意,舍去),x2=2,
∴P(2,3).
点评 此题主要考查了二次函数解析式的确定、抛物线的顶点坐标求法,图形面积的求法等知识,根据S△ABP=4S△COE列出方程是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.解不等式组:
(1)3x-3≤2(2x-1)
(2)$\left\{\begin{array}{l}{2x-1>5}\\{\frac{3x-7}{2}+1≤x}\end{array}\right.$.
(1)3x-3≤2(2x-1)
(2)$\left\{\begin{array}{l}{2x-1>5}\\{\frac{3x-7}{2}+1≤x}\end{array}\right.$.
4.计算(-2a3)2的结果是( )
| A. | -4a5 | B. | 4a5 | C. | -4a6 | D. | 4a6 |
1.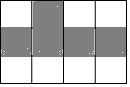 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{7}$ |
2.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
| A. | (-3,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
