题目内容
17.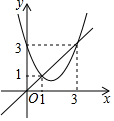 函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )
函数y=x2+bx+c与y=x的图象如图所示,则下列结论中正确的是( )| A. | 当1<x<3时,x2+(b-1)x+c<0 | B. | b+c=1 | ||
| C. | 3b+c=6 | D. | b2-4c>0 |
分析 由于抛物线与直线y=x相交于点(1,1),(3,3),则利用函数图象可得当1<x<3时,x2+bx+c<x,于是可对A进行判断;把(1,1)代入y=x2+bx+c可对B进行判断;把(3,3)代入y=x2+bx+c可对C进行判断;利用抛物线与x轴没有交点可对D进行判断.
解答 解:∵抛物线与直线y=x相交于点(1,1),(3,3),
∴当1<x<3时,x2+bx+c<x,
即x2+(b-1)x+c<0,所以A选项正确;
把(1,1)代入y=x2+bx+c得1+b+c=1,
∴b+c=0,所以B选项错误;
把(3,3)代入y=x2+bx+c得9+3b+c=3,
∴3b+c=6,所以C选项错误;
∵抛物线与x轴没有交点,
∴△=b2-4ac<0,所以D错误.
故选A.
点评 本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
7. 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
步骤1:分别以点A,D为圆心,以大于$\frac{1}{2}$AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:步骤1:分别以点A,D为圆心,以大于$\frac{1}{2}$AD的长为半径,在AD两侧作弧,两弧交于点M,N;
步骤2:连接MN,分别交AB,AC于点E,F;
步骤3:连接DE,DF.
下列叙述不一定成立的是( )
| A. | 线段DE是△ABC的中位线 | B. | 四边形AFDE是菱形 | ||
| C. | MN垂直平分线段AD | D. | $\frac{BD}{DC}$=$\frac{BE}{EA}$ |
12.在同一直角坐标系中,若直线y=k1x与双曲线y=$\frac{{k}_{2}}{x}$没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
9.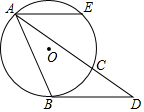 如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
 如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )
如图,AB、AC是⊙O的弦,过点B作⊙O的切线交AC的延长线于点D,点E是弧AC的中点,连接AE,若∠EAB=65°,则∠D的度数是( )| A. | 25° | B. | 50° | C. | 65° | D. | 70° |
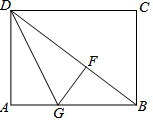 如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.
如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F.