题目内容
17.正方形的正投影不可能是( )| A. | 线段 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
分析 根据平行投影的特点:在同一时刻,平行物体的投影仍旧平行,即可得出答案.
解答 解:在同一时刻,平行物体的投影仍旧平行.得到的应是平行四边形或特殊的平行四边形或线段.
故正方形纸板ABCD的正投影不可能是梯形,
故选:D.
点评 此题主要考查了平行投影的性质,利用太阳光线是平行的,那么对边平行的图形得到的投影依旧平行是解题关键.

练习册系列答案
相关题目
7.解不等式组:
(1)3x-3≤2(2x-1)
(2)$\left\{\begin{array}{l}{2x-1>5}\\{\frac{3x-7}{2}+1≤x}\end{array}\right.$.
(1)3x-3≤2(2x-1)
(2)$\left\{\begin{array}{l}{2x-1>5}\\{\frac{3x-7}{2}+1≤x}\end{array}\right.$.
5. 如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )
如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )
 如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )
如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
12.已知△A′B′C′是由△ABC经过平移得到的,平移前后各顶点的坐标如下表所示.
(1)观察表中各对应点坐标的变化,并填空:a=0,b=2,c=9;
(2)在平面直角坐标系中画出△A'B'C'关于y轴对称的△A″B″C″.
| △ABC | A(a,0) | B(3,0) | C(5,5) |
| △A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
(2)在平面直角坐标系中画出△A'B'C'关于y轴对称的△A″B″C″.
2.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
| A. | (-3,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
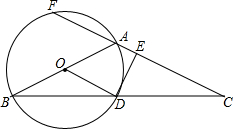 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F. 如图,已知点A是双曲线y=$\frac{{\sqrt{3}}}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是-3$\sqrt{3}$.
如图,已知点A是双曲线y=$\frac{{\sqrt{3}}}{x}$在第一象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值是-3$\sqrt{3}$.