题目内容
10.抛物线y=ax2+2x-5与x轴交于A、B两点,交y轴于点C,且∠ACB=90°,则a=$\frac{1}{5}$.分析 设A(m,0),B(n,0),由△AOC∽△COB,得$\frac{OA}{CO}$=$\frac{CO}{OB}$结合根与系数关系,列出方程即可解决问题
解答 解:∵抛物线y=ax2+2x-5与x轴交于A、B两点,交y轴于点C,
∴C(0,-5),设A(m,0),B(n,0),如图所示,
∵∠ACB=90°,
∴∠CAO+∠ABC=90°,∠ABC+∠OCB=90°,
∴∠OAC=∠OCB,∵∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴$\frac{OA}{CO}$=$\frac{CO}{OB}$,
∴$\frac{-m}{5}$=$\frac{5}{n}$,
∴mn=-25=-$\frac{5}{a}$,
∴a=$\frac{1}{5}$,
故答案为$\frac{1}{5}$.
点评 本题考查抛物线与x轴的交点、相似三角形的判定和性质、根与系数关系等知识,解题的关键是灵活应用这些知识解决问题,学会利用方程的思想思考问题,属于中考常考题型.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
20.已知n是奇数,m是偶数,关于x,y的二元一次方程组$\left\{\begin{array}{l}{2014x+15y=n}\\{2015x+18y=m}\end{array}\right.$,有整数解$\left\{\begin{array}{l}{x={x}_{0}}\\{y={y}_{0}}\end{array}\right.$,则( )
| A. | x0,y0均为偶数 | B. | x0,y0均为奇数 | ||
| C. | x0是偶数,y0是奇数 | D. | x0是奇数,y0是偶数 |

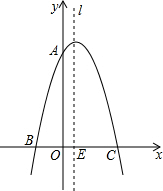 已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.
已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点. 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )
如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知E′D′=2,则BC的值是( )