题目内容
5.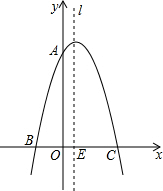 已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.
已知二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,点E是对称轴l与x轴的交点.(1)求二次函数的表达式;
(2)若在x轴上方的P点为抛物线上的动点,且∠BPC为锐角,直接写出PE的取值范围.
(3)T为y轴上一动点,且∠BPC=30°,求T点的坐标.
分析 (1)将B、C坐标代入抛物线的解析式中,通过联立方程组即可确定该抛物线的解析式.
(2)此题应该结合圆周角定理来理解,以E为圆心,BC为半径作圆,交抛物线于M、N两点,那么∠BMC=∠BNC=90°,若∠BEC是锐角,那么点E必在M、N之间的函数图象上,当P位于M或N得位置时,PE=3,当P位于抛物线的顶点时,PE的值为抛物线顶点纵坐标,由此可求得PE的取值范围;
(3)先作出等边三角形BCD,再结合圆周角定理来理解,以D为圆心,BC为半径作圆,和y轴交于点T,最后借助矩形的性质和垂径定理即可求出点T的坐标.
解答 解:(1)∵二次函数y=-x2+bx+c的图象与x轴交于B(-2,0),C(4,0)两点,
∴$\left\{\begin{array}{l}{-4-2b+c=0}\\{-16+4b+c=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{b=2}\\{c=8}\end{array}\right.$,
∴二次函数的表达式为y=-x2+2x+8,
(2)如图,
以E为圆心,BC长为直径作圆,交抛物线于M、N两点;
由圆周角定理知:∠BMC=∠BNC=90°,
此时ME=NE=$\frac{1}{2}$BC=3;
若∠BPC是锐角,那么点P必在M、N之间的抛物线图象上,故PE>3;
易知抛物线的顶点坐标为:(1,9),
当点P运动到抛物线的顶点位置时,PE的长最大,且此时PE=9;
综上可知,PE的取值范围为:3<PE≤9.
(3)如图2,
以BC为边在x轴上方作等边三角形,交直线l于点D,
再以点D为圆心BC为半径画圆,交y轴的正半轴于点T,
由圆周角定理知,∠BTC=$\frac{1}{2}$∠BDC=$\frac{1}{2}$×60°=30°,
在等边三角形BCD中,DT=BD=BC=6,
∴DE=$\frac{\sqrt{3}}{2}$BC=3$\sqrt{3}$,
过点D作DF⊥y轴于F,
∴四边形OEDF是矩形,
∴OF=DE=3$\sqrt{3}$,
∵二次函数的表达式为y=-x2+2x+8,
∴DF=OE=1,
在RtDFT中,FT=$\sqrt{D{T}^{2}-D{F}^{2}}$=$\sqrt{35}$
由垂径定理,得,OT=OF+FT=3$\sqrt{3}$+$\sqrt{35}$,
∴T(0,3$\sqrt{3}$+$\sqrt{35}$),
由对称性可知,T'(0,-3$\sqrt{3}$-$\sqrt{35}$),
即:T为y轴上一动点,且∠BPC=30°时,T点的坐标为(0,3$\sqrt{3}$+$\sqrt{35}$)或(0,-3$\sqrt{3}$-$\sqrt{35}$).
点评 此题是二次函数综合题,主要考查了二次函数解析式的确定、圆周角定理、矩形的性质,等边三角形的性质;涉及的知识点较多,综合性强,难度较大,解本题的关键是借助圆周角定理作出辅助线,也是解本题的难点.

| A. | y=x2 | B. | y=1-3x | C. | y=$\frac{1}{2x}$+2 | D. | y=$\sqrt{2}$ |
| A. | 等边三角形三条边相等 | B. | 三角形任何两边之和大于第三边 | ||
| C. | 三角形具有稳定性 | D. | 三角形内角和是180° |
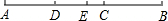 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )| A. | 8cm | B. | 12cm | C. | 14cm | D. | 10cm |
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
 如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD交BC于E点且∠AOD=120°,求∠AOE的度数.
如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD交BC于E点且∠AOD=120°,求∠AOE的度数.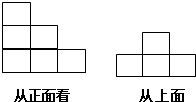 如图,是一个立体图形从两个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最多是( )
如图,是一个立体图形从两个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最多是( )