题目内容
10.阅读下面材料:能被7整除的数的特征为:数字去掉个位数,减去原个位数的2倍,计算得到的差能被7整除;如126,因为12-6×2=0,0能被7整除,所以I26能被7整除:
又如1001,因为100-1×2=98,9-8×2=-7,-7能被7整除,所以1001能被7整除;
根据阅读材料的方法,解答下列问题:
(1)如何判断364能否被7整除?
(2)一个三位数的百位数字是2,个位数字是7,如果这个三位数能被7整除,那么这个三位数是多少?
(3)说明为什么满足材料中特征的三位数可以被7整除.
分析 (1)根据能被7整除的数的特征即可求解;
(2)设三位数的十位数字是x,可得方程20+x-7×2=6+x,解方程即可求解;
(3)设三位数为100a+10b+c,可得10a+b-2c=7d(d为素数),得到100a+10b+c=70d+21c=7(10d+3c),从而求解.
解答 解:(1)因为36-4×2=28,28能被7整除,所以364能被7整除;
(2)设三位数的十位数字是x,
∵20+x-7×2=6+x,而这个三位数能被7整除,
∴6+x=7,或6+x=14,
解得x=1,或x=8,
故这个三位数是217或287;
(3)设三位数为100a+10b+c,依题意有
10a+b-2c=7d(d为素数),
则100a+10b-20c=70d,
100a+10b+c=70d+21c=7(10d+3c),
则100a+10b+c能被7整除.
点评 本题考查的是因式分解的应用,熟知能被7整除的数的特征:数字去掉个位数,减去原个位数的2倍,计算得到的差能被7整除是解答此题的关键.

练习册系列答案
相关题目
20.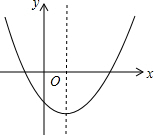 二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
 二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )| A. | a>0,b>0,c>0 | B. | a<0,b<0,c<0 | C. | a>0,b<0,c<0 | D. | a<0,b>0,c>0 |
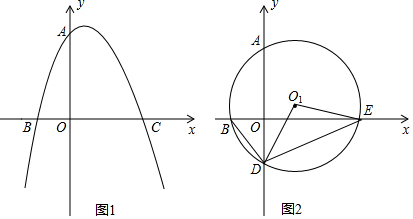
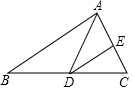 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC交BC于点D,点E是边AC上一点,连接DE,若∠ADE=40°,求证:DE∥AB.
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC交BC于点D,点E是边AC上一点,连接DE,若∠ADE=40°,求证:DE∥AB.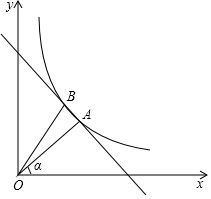 如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
 如图,已知∠ADE=∠B,∠CDE=∠BFG,求证:FG∥CD.
如图,已知∠ADE=∠B,∠CDE=∠BFG,求证:FG∥CD.