题目内容
18.甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1、2、3的小球,乙口袋中装有分别标有数字4、5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.请用列表或树状图的方法(只选其中一种)求出两个数字之和能被3整除的概率.分析 画树状图展示所有6种等可能的结果数,再找出数字之和能被3整除的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有6种等可能的结果数,其中两个数字之和能被3整除的结果数为2,
所以两个数字之和能被3整除的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.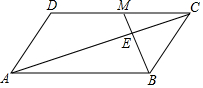 如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
 如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )
如图,在?ABCD中,∠ABC的平分线与对角线AC交于点E,与CD交于点M,已知BC=2,DM=3,?ABCD的面积为28,则△ABE的面积为( )| A. | $\frac{28}{3}$ | B. | $\frac{21}{2}$ | C. | 10 | D. | $\frac{14}{3}$ |
 作图题:如图△ABC,作出关于直线l轴对称的图形.
作图题:如图△ABC,作出关于直线l轴对称的图形.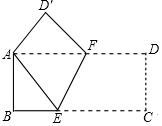 按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.
按如图方式折叠长方形纸片ABCD,使顶点A、C重合(图中点D落在点D′处,E,F分别是折痕与BC,AD的交点),已知AB=3,BC=9,求BE及折痕EF的长.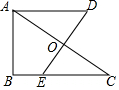 如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.
如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$. 如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,与y轴相交于点C,点P是抛物线上一点,过点P作PD∥y轴交线段BC干点D.
如图,抛物线y=ax2+bx+3经过A(-1,0),B(3,0)两点,与y轴相交于点C,点P是抛物线上一点,过点P作PD∥y轴交线段BC干点D.