题目内容
5．
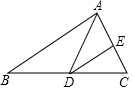如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC交BC于点D，点E是边AC上一点，连接DE，若∠ADE=40°，求证：DE∥AB．
分析 先根据三角形内角和定理求出∠BAC的度数，再由角平分线的性质求出∠BAD的度数，根据平行线的判定即可得出结论．
解答 证明：∵在△ABC中，∠B=46°，∠C=54°，
∴∠BAC=180°-46°-54°=80°．
∵AD平分∠BAC，
∴∠BAD=$\frac{1}{2}$∠BAC=40°．
∵∠ADE=∠BAD=40°．
∴DE∥AB．
点评 本题考查的是等腰三角形的性质和判定，平行线的判定，熟练掌握等腰三角形的判定和性质是解题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
15．在Rt△ABC中，∠C=90°，AC=8，BC=6，则cosB的值是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |
20．
如图，∠1=45°，∠3=105°，则∠2的度数为（ ）
如图，∠1=45°，∠3=105°，则∠2的度数为（ ）| A． | 60° | B． | 55° | C． | 35° | D． | 30° |
17．已知∠A是锐角，且cosA=$\frac{\sqrt{3}}{2}$，那么∠A等于（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
吉安市机关公车改革于今年4月1日正式开始实施，小明坐着爸爸新买的小车，在闹市区街道边发现一块标志牌（如图所示），小明知道这表示车速不超过这个字，请你用式子表示在该车道上车辆行驶速度v（km/h）的数值范围：v≤10．