��Ŀ����
1����ͼ1����֪���κ���y=-x2+bx+c��ͼ����M��-2��-4������x�ύ�ڵ�B��-1��0���͵�C��y�ύ��A�㣮��1������κ����Ľ���ʽ��
��2����x���ϴ���һ��N��ʹ�á�NMC=��BAC�����N�����꣮
��3����ͼ2�����D��y�Ḻ������һ���㣬��A��B��D����ġ�O1��x������һ��E������BD��DE��O1E������D��y�Ḻ�������˶�ʱ����S${\;}_{��{O}_{1}DE}$��S��BOD��ֵ��
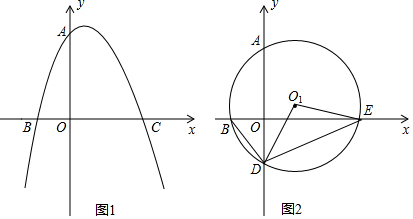
���� ��1�����ô���ϵ�������ɼ��ɽ�����⣮
��2����ͼ1�У�����AB��AC����MD��x����D������֤����OAC=��DMC=45�㣬��֤����AOB�ס�MDN���Ƴ�$\frac{OA}{DM}$=$\frac{OB}{DN}$�����DN=2�����ɽ�����⣮
��3����ͼ3�У�����AB����O1N��DE��N���ɡ�AOB�ס�EOD���Ƴ�$\frac{AO}{OE}$=$\frac{OB}{OD}$���Ƴ�OE=2OD����OD=k����OE=2k��DE=$\sqrt{5}$k���ɡ�BOD�ס�O1ND���Ƴ�$\frac{{S}_{��D{O}_{1}N}}{{S}_{��BOD}}$=��$\frac{DN}{OD}$��2=��$\frac{\frac{\sqrt{5}}{2}k}{k}$��2=$\frac{5}{4}$���ɴ˼��ɽ�����⣮
��� �⣺��1����M��-2��-4����B��-1��0�����������y=-x2+bx+c�õ�$\left\{\begin{array}{l}{-4-2b+c=-4}\\{-1-b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$��
�������ߵĽ���ʽΪy=-x2+x+2��
��2����ͼ1�У�����AB��AC����MD��x����D��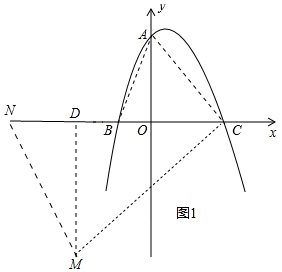
����������y=-x2+x+2����y=0��-x2+x+2=0�����x=-1��2��
��C��2��0����
��OA=OC=2��DM=DC=4��
���OAC=��DMC=45�㣬
�ߡ�NMC=��BAC��
���NMD=��BAO���ߡ�AOB=��MDN=90�㣬
���AOB�ס�MDN��
��$\frac{OA}{DM}$=$\frac{OB}{DN}$��
��$\frac{2}{4}$=$\frac{1}{DN}$��
��DN=2��
��ON=4��
���N��������-4��0����
��3����ͼ3�У�����AB����O1N��DE��N��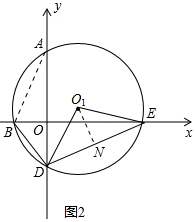
�ߡ�AOB=��DOE����BAO=��OED��
���AOB�ס�EOD��
��$\frac{AO}{OE}$=$\frac{OB}{OD}$��
��$\frac{2}{OE}$=$\frac{1}{OD}$��
��OE=2OD����OD=k����OE=2k��DE=$\sqrt{5}$k��
��O1N��DE��
��DN=EN����DO1N=��EO1N��
�ߡ�DO1E=2��DBE��
���OBD=��DO1N��
�ߡ�BOD=��O1ND=90�㣬
���BOD�ס�O1ND��
��$\frac{{S}_{��D{O}_{1}N}}{{S}_{��BOD}}$=��$\frac{DN}{OD}$��2=��$\frac{\frac{\sqrt{5}}{2}k}{k}$��2=$\frac{5}{4}$��
��${S}_{��{O}_{1}DE}$=2${S}_{��D{O}_{1}N}$��
��$\frac{{S}_{��D{O}_{1}E}}{{S}_{��BOD}}$=$\frac{10}{4}$=$\frac{5}{2}$��
���� ���⿼����κ����ۺ��⡢����ֱ�������ε����ʡ����������ε��ж������ʡ����ɶ�������������֪ʶ������Ĺؼ�����ȷѰ�����������ν�����⣬�����п�ѹ���⣮

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�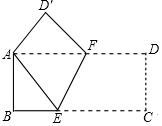 ����ͼ��ʽ�۵�������ֽƬABCD��ʹ����A��C�غϣ�ͼ�е�D���ڵ�D�䴦��E��F�ֱ����ۺ���BC��AD�Ľ��㣩����֪AB=3��BC=9����BE���ۺ�EF�ij���
����ͼ��ʽ�۵�������ֽƬABCD��ʹ����A��C�غϣ�ͼ�е�D���ڵ�D�䴦��E��F�ֱ����ۺ���BC��AD�Ľ��㣩����֪AB=3��BC=9����BE���ۺ�EF�ij���