题目内容
20．
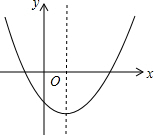二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（ ）| A． | a＞0，b＞0，c＞0 | B． | a＜0，b＜0，c＜0 | C． | a＞0，b＜0，c＜0 | D． | a＜0，b＞0，c＞0 |
分析 根据图象开口、对称轴位置，与y轴交点的位置即可判断a、b、c与0的大小．
解答 解：由图象可知：
开口向上，故a＞0，
对称轴x=-$\frac{b}{2a}$＞0，故b＜0，
图象与y轴的交点在x轴下方，故c＜0，
故选（C）
点评 本题考查二次函数的图象性质，解题的关键是根据抛物线的开口方向、对称轴位置，与y轴交点的位置来判断，本题属于基础题型．
练习册系列答案
名校课堂系列答案
相关题目
作图题：如图△ABC，作出关于直线l轴对称的图形．
15．在Rt△ABC中，∠C=90°，AC=8，BC=6，则cosB的值是（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{3}{4}$ | D． | $\frac{4}{3}$ |