题目内容
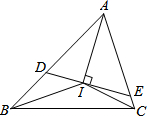 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.(1)若∠BAC=70°,∠BIC的度数为
(2)根据(1)的解题经验你发现了∠BIC与哪些角相等,请写出来,并说明其中的道理.
(3)图中与∠EIC相等的角有
考点:三角形内角和定理
专题:
分析:(1)根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠IBC+∠ICB,然后在△BCI中利用三角形的内角和定理列式计算即可得解;
(2)用∠A表示出∠BIC,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BDI和∠CEI即可判断;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BIC+∠EIC=∠BDI+∠DBI,即可得到∠EIC=∠DBI,再根据角平分线的定义可得∠DBI=∠IBC.
(2)用∠A表示出∠BIC,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BDI和∠CEI即可判断;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BIC+∠EIC=∠BDI+∠DBI,即可得到∠EIC=∠DBI,再根据角平分线的定义可得∠DBI=∠IBC.
解答:解:(1)由三角形的内角和定理,∠ABC+∠ACB=180°-∠A,
∵△ABC的三条内角平分线相交于点I,
∴∠IBC+∠ICB=
(∠ABC+∠ACB)=
(180°-∠A),
在△BCI中,∠BIC=180°-(∠IBC+∠ICB)=180°-
(180°-∠A)=90°+
∠A,
∵∠BAC=70°,
∴∠BIC=90°+
×70°=125°;
(2)∵DE⊥AI,
∴∠AID=∠AIE=90°,
∵AI平分∠BAC,
∴∠DAI=∠EAI=
∠A,
∴∠BDI=90°+
∠A,∠CEI=90°+
∠A,
∴与∠BIC相等的角有∠BDI、∠CEI;
(3)由三角形的外角性质得,∠BIC+∠EIC=∠BDI+∠DBI,
∵∠BIC=∠BDI,
∴∠EIC=∠DBI,
∵BI平分∠ABC,
∴∠DBI=∠IBC,
∴与∠EIC相等的角有∠DBI、∠IBC.
故答案为:(1)125°;(3)∠DBI、∠IBC.
∵△ABC的三条内角平分线相交于点I,
∴∠IBC+∠ICB=
| 1 |
| 2 |
| 1 |
| 2 |
在△BCI中,∠BIC=180°-(∠IBC+∠ICB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BAC=70°,
∴∠BIC=90°+
| 1 |
| 2 |
(2)∵DE⊥AI,
∴∠AID=∠AIE=90°,
∵AI平分∠BAC,
∴∠DAI=∠EAI=
| 1 |
| 2 |
∴∠BDI=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∴与∠BIC相等的角有∠BDI、∠CEI;
(3)由三角形的外角性质得,∠BIC+∠EIC=∠BDI+∠DBI,
∵∠BIC=∠BDI,
∴∠EIC=∠DBI,
∵BI平分∠ABC,
∴∠DBI=∠IBC,
∴与∠EIC相等的角有∠DBI、∠IBC.
故答案为:(1)125°;(3)∠DBI、∠IBC.
点评:本题考查了三角形的内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并综合运用,准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
 已知AB为⊙O的直径,
已知AB为⊙O的直径,

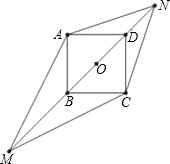 如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且
如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且
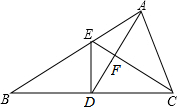 如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:AB•FD=AC•FC.
如图,已知在△ABC中,D是BC的中点,且AD=AC,DE⊥BC交AB于点E,EC与AD相交于点F.求证:AB•FD=AC•FC. 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.