题目内容
 如图是甲、乙两人同一地点出发后,路程随时间变化的图象.
如图是甲、乙两人同一地点出发后,路程随时间变化的图象.(1)此变化过程中,
(2)甲的速度
(3)6时表示
(4)路程为150km,甲行驶了
(5)9时甲在乙的
(6)乙比甲先走了3小时,对吗?
考点:函数的图象
专题:
分析:(1)根据自变量与因变量的含义得到时间是自变量,路程是因变量;
(2)甲走6行驶100千米,乙走3小时行驶了100千米,则可得到它们的速度的大小;
(3)6时两图象相交,说明他们相遇;
(4)观察图象得到路程为150km,甲行驶9小时;乙行驶了7-3=4小时;
(5)观察图象得到t=9时,乙的图象在甲的上方,即乙行驶的路程远些;
(6)观察图象得到甲先出发3小时后,乙才开始出发.
(2)甲走6行驶100千米,乙走3小时行驶了100千米,则可得到它们的速度的大小;
(3)6时两图象相交,说明他们相遇;
(4)观察图象得到路程为150km,甲行驶9小时;乙行驶了7-3=4小时;
(5)观察图象得到t=9时,乙的图象在甲的上方,即乙行驶的路程远些;
(6)观察图象得到甲先出发3小时后,乙才开始出发.
解答:解:(1)函数图象反映路程随时间变化的图象,则t是自变量,s为因变量;
(2)甲的速度=
=
千米/小时,乙的速度=
千米/小时,所以甲的速度小于乙的速度;
(3)6时表示他们相遇,即乙追赶上了甲;
(4)路程为150km,甲行驶9小时;乙行驶了7-3=4小时;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面
(6)不对,是乙比甲晚走了3小时.
故答案为:(1)t,s;(2)小于;(3)乙追赶上了甲;(4)9,4;(5)后面;(6)不对.
(2)甲的速度=
| 100 |
| 6 |
| 50 |
| 3 |
| 100 |
| 3 |
(3)6时表示他们相遇,即乙追赶上了甲;
(4)路程为150km,甲行驶9小时;乙行驶了7-3=4小时;
(5)t=9时,乙的图象在甲的上方,即乙行驶的路程远些,所以9时甲在乙的后面
(6)不对,是乙比甲晚走了3小时.
故答案为:(1)t,s;(2)小于;(3)乙追赶上了甲;(4)9,4;(5)后面;(6)不对.
点评:本题考查了函数图象:利用函数图象反映两变量之间的变化规律,通过该规律解决有关的实际问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
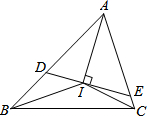 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.