题目内容
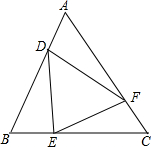
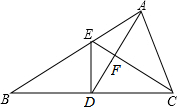如图，已知在△ABC中，D是BC的中点，且AD=AC，DE⊥BC交AB于点E，EC与AD相交于点F．求证：AB•FD=AC•FC．考点：相似三角形的判定与性质
专题：证明题
分析：若要证明AB•FD=AC•FC，则可转为以上线段所在的两个三角形相似，即△ABC∽△FCD即可．
解答：证明：∵AD=AC，
∴∠ADC=∠ACD，
∵D是BC的中点，ED⊥BC，
∴BE=EC，
∴∠ABC=∠ECD，
∴△ABC∽△FCD，
∴
=
，
即AB•FD=AC•FC．
∴∠ADC=∠ACD，
∵D是BC的中点，ED⊥BC，
∴BE=EC，
∴∠ABC=∠ECD，
∴△ABC∽△FCD，
∴
| AB |
| FC |
| AC |
| FD |
即AB•FD=AC•FC．
点评：本题考查了相似三角形的判定和性质，用的知识点有等腰三角形的性质、垂直平分线的性质，题目的综合性较强，难度不大．
练习册系列答案
相关题目
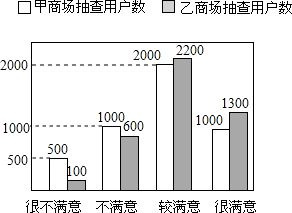在“3.15”消费者权益日的活动中，对甲、乙两家商场售后服务的满意度进行了抽查．如图反映了被抽查用户对两家商场售后服务的满意程度（以下称：用户满意度），分为很不满意、不满意、较满意、很满意四个等级．
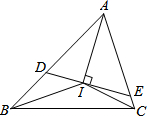我们知道，任何一个三角形的三条内角平分线相交于一点，如图，若△ABC的三条内角平分线相交于点I，过I作DE⊥AI分别交AB、AC于点D、E．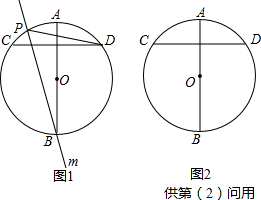
△ABC是等边三角形，且AD=BE=CF．那么△DEF是等边三角形吗？