题目内容
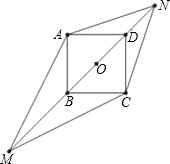 如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且AM=
如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且AM=| 5 |
(1)求证:△ADN∽△MBA;
(2)求四边形AMCN的面积.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)运用正方形对解线及三角形外角性质得出对应角相等,得出△ADN∽△MBA;
(2)连AO,可得出OA,OB及MB的长,再运用△ADN∽△MBA得出DN的长,利用三角形面积公式求出四边形AMCN的面积.
(2)连AO,可得出OA,OB及MB的长,再运用△ADN∽△MBA得出DN的长,利用三角形面积公式求出四边形AMCN的面积.
解答:(1)证明:∵∠ABM=∠NDA=135°,
∴∠NAD=∠MAN-∠DAB-∠MAB=135°-90°-∠MAB=45°-∠MAB,
∵∠AMB=45°-∠MAB,
∴∠NAD=∠AMB
∵∠ADN=∠ABM=135°,
∴△ADN∽△MBA
 (2)解:设正方形ABCD的中心为O,连AO,则
(2)解:设正方形ABCD的中心为O,连AO,则
AO⊥BD,AO=OB=
,MO=
=
=
,
∴MB=MO-OB=
.
∵△ADN∽△MBA
∴
=
,
∴DN=
•BA=
×1=
.
根据对称性可知,四边形AMCN的面积S=2S△MAN=2×
×MN×AO=2×
×(
+
+
)×
=
.
∴∠NAD=∠MAN-∠DAB-∠MAB=135°-90°-∠MAB=45°-∠MAB,
∵∠AMB=45°-∠MAB,
∴∠NAD=∠AMB
∵∠ADN=∠ABM=135°,
∴△ADN∽△MBA
 (2)解:设正方形ABCD的中心为O,连AO,则
(2)解:设正方形ABCD的中心为O,连AO,则AO⊥BD,AO=OB=
| ||
| 2 |
| AM2-AO2 |
(
|
3
| ||
| 2 |
∴MB=MO-OB=
| 2 |
∵△ADN∽△MBA
∴
| AD |
| MB |
| DN |
| BA |
∴DN=
| AD |
| MB |
| 1 | ||
|
| ||
| 2 |
根据对称性可知,四边形AMCN的面积S=2S△MAN=2×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
点评:本题主要考查了相似三角形的判定与性质及正方形的性质,解题的关键是运用三角形相似求出DN的长度.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
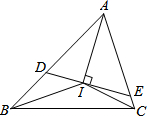 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.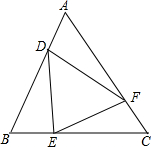 △ABC是等边三角形,且AD=BE=CF.那么△DEF是等边三角形吗?
△ABC是等边三角形,且AD=BE=CF.那么△DEF是等边三角形吗?