题目内容
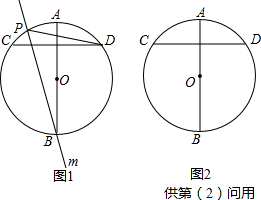
如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s,过点P作PE∥AC交DC于点E,同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,连接PQ、QE,PQ与AC交与点F,设运动时间为t(s)(0<t<8).
(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的
;
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.

(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的
| 9 |
| 32 |
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.

考点:四边形综合题
专题:
分析:(1)四边形PFCE是平行四边形则PD=CQ,据此即可得到关于t的方程,即可求解;
(2)用t表示出PD、EC、DE、CQ的长,则四边形DPQC、△PDE以及△QCE的面积可用t表示,则进一步表示出△PQE的面积,从而得到函数解析式;
(3)根据△PQE的面积为矩形ABCD面积的
即可列方程求解;
(4)点E在线段PQ的垂直平分线上,则PE=QE,然后根据勾股定理表示出PE2和QE2,即可列方程求得t的值.
(2)用t表示出PD、EC、DE、CQ的长,则四边形DPQC、△PDE以及△QCE的面积可用t表示,则进一步表示出△PQE的面积,从而得到函数解析式;
(3)根据△PQE的面积为矩形ABCD面积的
| 9 |
| 32 |
(4)点E在线段PQ的垂直平分线上,则PE=QE,然后根据勾股定理表示出PE2和QE2,即可列方程求得t的值.
解答:解:(1)PD=8-t,CQ=2t,
根据题意得:8-t=2t,
解得:t=
;
(2)S四边形PDCQ=
(PD+CQ)•CD=
×6(8-t+2t)=3t(8+t)=3t2+24t,
∵PE∥AC,
∴
=
,
∴
=
,
则DE=-
t+6,
则EC=6-(-
t+6)=
t,
则S△PDE=
PD•DE=
(8-t)•(-
t+6),
S△CQE=
CQ•EC=
×2t•
t=
t2,
则s=3t2+24t-
(8-t)•(-
t+6)-
t2,
即s=
t2+30t-24;
(3)S矩形ABCD=6×8=48,
根据由题意得:
t2+30t-24=
×48,即t2+16t-20=0,
解得:t=2
-8或-2
-8(舍去).
则t=2
-8;
(4)在直角△PDE中,PD2=(8-t)2+(-
t+6)2,
在直角△COQ中,QE2=(2t)2+(
t)2,
当点E在线段PQ的垂直平分线上时,PD2=QE2,
则(8-t)2+(-
t+6)2=(2t)2+(
t)2,
解得:t=
或
(舍去).
则t=
.
根据题意得:8-t=2t,
解得:t=
| 8 |
| 3 |
(2)S四边形PDCQ=
| 1 |
| 2 |
| 1 |
| 2 |
∵PE∥AC,
∴
| PD |
| AD |
| DE |
| DC |
∴
| 8-t |
| 8 |
| DE |
| 6 |
则DE=-
| 3 |
| 4 |
则EC=6-(-
| 3 |
| 4 |
| 3 |
| 4 |
则S△PDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
S△CQE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
则s=3t2+24t-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
即s=
| 15 |
| 8 |
(3)S矩形ABCD=6×8=48,
根据由题意得:
| 15 |
| 8 |
| 9 |
| 32 |
解得:t=2
| 21 |
| 21 |
则t=2
| 21 |
(4)在直角△PDE中,PD2=(8-t)2+(-
| 3 |
| 4 |
在直角△COQ中,QE2=(2t)2+(
| 3 |
| 4 |
当点E在线段PQ的垂直平分线上时,PD2=QE2,
则(8-t)2+(-
| 3 |
| 4 |
| 3 |
| 4 |
解得:t=
-25+5
| ||
| 6 |
-25-5
| ||
| 6 |
则t=
-25+5
| ||
| 6 |
点评:本题考查了平行线分线段成比例定理,以及勾股定理,正确解方程是解决本题的关键.

练习册系列答案
相关题目
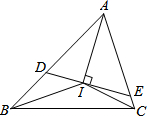 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.