题目内容
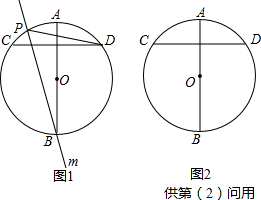
已知:在△ABC中,∠C=90°,F为射线BA上一点,且满足CB2=CE•CA,过B作BD⊥DF于D,交AC边于E,
(1)如图1,证明2∠CBD=∠BFD.
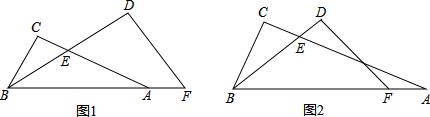
(2)如图2,点F在线段AB上时,若BC:AE=
,试探究线段BD与DF间的数量关系,并证明你的结论.

(1)如图1,证明2∠CBD=∠BFD.
(2)如图2,点F在线段AB上时,若BC:AE=
| 3 |
| 5 |
考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)作AH⊥BD,交BD于点H,由比例式可求得△BCE∽△ACB,得出∠CBD=∠CAB,利用直角三角形得出∠CBD=∠CAH,由平行线得出2∠CBD=∠BFD.
(2)延长BC至点G,使CG=BC,连接AG交BD延长线于点M,连接GE并延长交AB于点K,由△ACG≌△ACB得出∠CAG=∠CAB,BC=CG,由∠BFD=2∠CAB,得出FD∥AM,再由△BGM∽△AEM得出
=
=
,由△GME∽△BDF,得出
=
=
,从而得到BD与DF间的数量关系.
(2)延长BC至点G,使CG=BC,连接AG交BD延长线于点M,连接GE并延长交AB于点K,由△ACG≌△ACB得出∠CAG=∠CAB,BC=CG,由∠BFD=2∠CAB,得出FD∥AM,再由△BGM∽△AEM得出
| BG |
| AE |
| GM |
| EM |
| 6 |
| 5 |
| BD |
| DF |
| GM |
| EM |
| 6 |
| 5 |
解答:解:如图1,作AH⊥BD,交BD于点H,

∵CB2=CE•CA,即
=
,
∴△BCE∽△ACB,
∴∠CBD=∠CAB,
∵∠BCE=∠AHE,∠CEB=∠HEA,
∴∠CBD=∠CAH,
∴2∠CBD=∠BAH,
∵AH∥DF,
∴∠BAH=∠BFD,
∴2∠CBD=∠BFD,
(2)如图2,延长BC至点G,使CG=BC,连接AG交BD延长线于点M,连接GE并延长交AB于点K,

在△ACG和△ACB中,
∴△ACG≌△ACB(SAS)
∴∠CAG=∠CAB,BC=CG,
∴BC=
BG,
∵CB2=CE•CA,即
=
,
∴△BCE∽△ACB,
∴∠CBD=∠CAB,
∵∠CBD+∠CAB+∠DBF=∠BFD+∠DBF=90°,
∴∠BFD=2∠CAB,
∴∠BFD=∠GAB,
∴FD∥AM,可得∠AMB=90°,
∵∠CBD=∠CAB,
∴∠CBD=∠CAG,
∴△BGM∽△AEM,
∴
=
,
∵BC:AE=
,
∴
=
=
,
∵CG=BC,EC⊥BG,
∴GE=BE,
∴∠CBD=∠CGE,
∵∠CBD=∠CAB,
∴∠CGE=∠CAB,
∵∠CEG=∠KEA,
∴∠EKA=∠GCE=90°,
∵∠GEM=∠BEK,∠GME=∠BKE=90°,
∴∠EGM=∠FBD,
∴△GME∽△BDF,
∴
=
=
,
∴BD=
DF.

∵CB2=CE•CA,即
| CB |
| CE |
| CA |
| CB |
∴△BCE∽△ACB,
∴∠CBD=∠CAB,
∵∠BCE=∠AHE,∠CEB=∠HEA,
∴∠CBD=∠CAH,
∴2∠CBD=∠BAH,
∵AH∥DF,
∴∠BAH=∠BFD,
∴2∠CBD=∠BFD,
(2)如图2,延长BC至点G,使CG=BC,连接AG交BD延长线于点M,连接GE并延长交AB于点K,

在△ACG和△ACB中,
|
∴△ACG≌△ACB(SAS)
∴∠CAG=∠CAB,BC=CG,
∴BC=
| 1 |
| 2 |
∵CB2=CE•CA,即
| CB |
| CE |
| CA |
| CB |
∴△BCE∽△ACB,
∴∠CBD=∠CAB,
∵∠CBD+∠CAB+∠DBF=∠BFD+∠DBF=90°,
∴∠BFD=2∠CAB,
∴∠BFD=∠GAB,
∴FD∥AM,可得∠AMB=90°,
∵∠CBD=∠CAB,
∴∠CBD=∠CAG,
∴△BGM∽△AEM,
∴
| BG |
| AE |
| GM |
| EM |
∵BC:AE=
| 3 |
| 5 |
∴
| BG |
| AE |
| GM |
| EM |
| 6 |
| 5 |
∵CG=BC,EC⊥BG,
∴GE=BE,
∴∠CBD=∠CGE,
∵∠CBD=∠CAB,
∴∠CGE=∠CAB,
∵∠CEG=∠KEA,
∴∠EKA=∠GCE=90°,
∵∠GEM=∠BEK,∠GME=∠BKE=90°,
∴∠EGM=∠FBD,
∴△GME∽△BDF,
∴
| BD |
| DF |
| GM |
| EM |
| 6 |
| 5 |
∴BD=
| 6 |
| 5 |
点评:本题主要考查了相似三角形的判定与性质和全等三角形的判定与性质,解题的关键是正确作出辅助线利用三角形相似找出线段的关系,难度很大.

练习册系列答案
相关题目
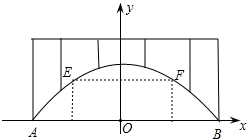 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知抛物线的函数表达式为y=-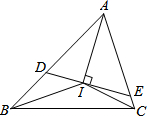 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.