题目内容
 已知AB为⊙O的直径,
已知AB为⊙O的直径, |
| AD |
 |
| DC |
(1)求证:AF=DF.
(2)若AB=10,AC=6,求AF长.
考点:相似三角形的判定与性质,垂径定理,圆周角定理
专题:
分析:(1)连接BD,利用直角三角形求出∠ADE=∠ABD,再利用
=
,得出∠DAF=∠ABD,∠DAF=∠ADE,即可得出结论AF=DF.
(2)连接OD,可得OD⊥AC,由已知得出AM,OM的长,由△DEO≌△AMO得出OE的长,即可得到AE的长,由△AEF∽△AMO,利用比例式求出AF的长.
 |
| AD |
 |
| DC |
(2)连接OD,可得OD⊥AC,由已知得出AM,OM的长,由△DEO≌△AMO得出OE的长,即可得到AE的长,由△AEF∽△AMO,利用比例式求出AF的长.
解答:(1)证明:如图1,连接BD,

∵AB是⊙O直径,
∴∠ADB=90°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠ADE+∠DAB=90°,∠DAE+∠ABD=90°,
∴∠ADE=∠ABD,
∵弧AD=弧DC,
∴∠DAF=∠ABD,
∵∠ABD=∠C,
∴∠DAF=∠ADE,
∴AF=DF;
(2)解:如图2,连接OD,交AC于点M,

∵
=
,
∴OD⊥AC,
∵AB=10,AC=6,
∴AM=3,OM=
=
=4,
在△DEO和△AMO中,
,
∴△DEO≌△AMO(AAS)
∴OE=OM=4,
∴AE=5-4=1,
∵∠DEA=∠OMA=90°,
∴△AEF∽△AMO,
∴
=
,即
=
,
∴AF=
.

∵AB是⊙O直径,
∴∠ADB=90°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠ADE+∠DAB=90°,∠DAE+∠ABD=90°,
∴∠ADE=∠ABD,
∵弧AD=弧DC,
∴∠DAF=∠ABD,
∵∠ABD=∠C,
∴∠DAF=∠ADE,
∴AF=DF;
(2)解:如图2,连接OD,交AC于点M,

∵
 |
| AD |
 |
| DC |
∴OD⊥AC,
∵AB=10,AC=6,
∴AM=3,OM=
| AO2-AM2 |
| 52-32 |
在△DEO和△AMO中,
|
∴△DEO≌△AMO(AAS)
∴OE=OM=4,
∴AE=5-4=1,
∵∠DEA=∠OMA=90°,
∴△AEF∽△AMO,
∴
| AE |
| AM |
| AF |
| AO |
| 1 |
| 3 |
| AF |
| 5 |
∴AF=
| 5 |
| 3 |
点评:本题考查了圆周角定理,相似三角形的性质和判定,等腰三角形的判定的应用,主要考查学生运用定理进行推理的能力,注意:在同圆中,等弧所对的圆周角相等,题目比较好,但是有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,直线AB∥CD,∠B=70°,∠C=25°,则∠E等于( )
如图,直线AB∥CD,∠B=70°,∠C=25°,则∠E等于( )| A、85° | B、75° |
| C、70° | D、65° |
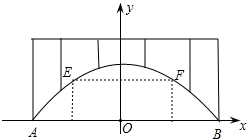 廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知抛物线的函数表达式为y=-
廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知抛物线的函数表达式为y=-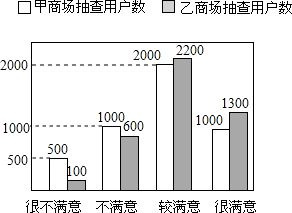 在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级.
在“3.15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级.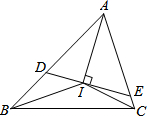 我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.
我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.