题目内容
20.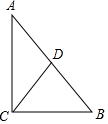 如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.
分析 由条件可先求得∠BCD=30°,利用直角三角形的性质可求得BD:BC=1:2;由勾股定理可求得AC,由△ABC∽△CBD,可求得BD和CD.
解答 解:
∵CD⊥AB,
∴∠CDB=90°,
①若∠A=30°,则∠B=60°,
∴∠BCD=30°,
∴BD:BC=1:2;
②若BC=6,AB=10,则AC=8,
∵∠BDC=∠ACB=90°,∠B=∠B,
∴△ABC∽△CBD,
∴$\frac{BC}{BD}$=$\frac{AB}{BC}$=$\frac{AC}{CD}$,即$\frac{6}{BD}$=$\frac{10}{6}$=$\frac{8}{CD}$,
∴BD=3.6,CD=4.8;
故答案为:1:2;3.6;4.8.
点评 本题主要考查直角三角形的性质及相似三角形的判定和性质,掌握直角三角形中30°所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
 如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=10:5:3,则∠α的度数为160°.
如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=10:5:3,则∠α的度数为160°.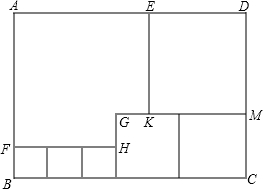 如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=x cm,
如图所示,用三种大小不同的六个正方形和一个缺角的长方形拼成长方形ABCD,其中,GH=2cm,GK=2cm,设BF=x cm,