题目内容
15．若$\frac{a-2b}{2a+b}$=$\frac{1}{5}$，则$\frac{a}{b}$=$\frac{11}{3}$；若a：b：c=3：2：5，则$\frac{a+2b-c}{a-b+c}$=$\frac{1}{3}$．分析 由$\frac{a-2b}{2a+b}$=$\frac{1}{5}$得：a=$\frac{11}{3}$b，把它们代入原式合并后约分即可，由a：b：c=3：2：5，设a=3k，b=2k，c=5k，然后把它们代入原式合并后约分即可．
解答 解：由$\frac{a-2b}{2a+b}$=$\frac{1}{5}$得：a=$\frac{11}{3}$b，$\frac{a}{b}$=$\frac{\frac{11}{3}b}{b}$=$\frac{11}{3}$，
由a：b：c=3：2：5，设a=3k，b=2k，c=5k，则$\frac{a+2b-c}{a-b+c}$=$\frac{2k}{6k}$=$\frac{1}{3}$，
故答案为：$\frac{11}{3}$，$\frac{1}{3}$．
点评 本题考查了比例的性质：内项之积等于外项之积；合比性质；分比性质；合分比性质；等比性质．
练习册系列答案
相关题目
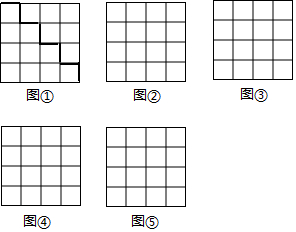如图（1），把大小为4×4的正方形方格图形分割成两个全等图形，请在图中，沿着虚线画出四种不同的分法，把4×4的正方形方格图形分割成两个全等图形．
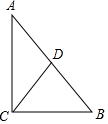如图，△ABC中，∠ACB=90°，CD⊥AB于D，若∠A=30°，则BD：BC=1：2；若BC=6，AB=10，则BD=3.6，CD=4.8．
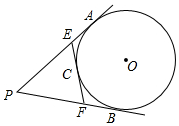如图，PA，PB是圆O的切线，切点为分别A，B，圆O的切线EF分别交PA，PB于点E，F，切点C在弧$\widehat{AB}$上，若PA长为2，则△PEF的周长是4．