题目内容
5.计算或解关于x的方程(1)计算:(-2)2-(2-$\sqrt{3}$)0+2×$\sqrt{12}$;
(2)先将$\frac{{x}^{2}+2x}{x-1}$•(1-$\frac{1}{x}$)化简,然后请自选一个你喜欢的x值,再求原式的值.
(3)x2+3x-10=0
(4)1+$\frac{3}{3-x}$=$\frac{4-x}{x-3}$.
分析 (1)先根据零指数幂的意义计算,然后计算乘方运算和二次根式的化简;
(2)先把括号内通分,再进行约分得到原式=x+2,然后取一个使原式有意义的一个x的值代入计算即可;
(3)利用因式分解法解方程;
(4)先去分母,把分式方程化为整式方程,解整式方程,然后检验确定原方程的解.
解答 解:(1)原式=4-1+4$\sqrt{3}$
=3+4$\sqrt{3}$;
(2)原式=$\frac{x(x+2)}{x-1}$•$\frac{x-1}{x}$
=x+2,
当x=2时,原式=2+2=4;
(3)(x+5)(x-2)=0,
所以x1=-5,x2=2;
(4)去分母得x-3-3=4-x,
解得x=5,
检验:当x=5时,x-3≠0,
所以原方程的解为x=5.
点评 本题考查了解一元二次方程-因式分解法:就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了实数的运算和解分式方程.

练习册系列答案
相关题目
10. 如图,△ABC≌△EDF,AE=20,FC=10,则AF的长是( )
如图,△ABC≌△EDF,AE=20,FC=10,则AF的长是( )
 如图,△ABC≌△EDF,AE=20,FC=10,则AF的长是( )
如图,△ABC≌△EDF,AE=20,FC=10,则AF的长是( )| A. | 5 | B. | 10 | C. | 15 | D. | 不能确定 |
 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、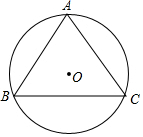 求正三角形的内切圆半径、外接圆半径和高的比.
求正三角形的内切圆半径、外接圆半径和高的比.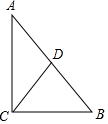 如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,若∠A=30°,则BD:BC=1:2;若BC=6,AB=10,则BD=3.6,CD=4.8.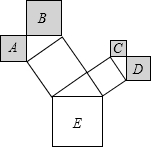 如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.