题目内容
16.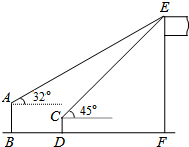 如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
分析 过点A作AM⊥EF于点M,过点C作CN⊥EF于点N.设CN=x,分别表示出EM、AM的长度,然后在Rt△AEM中,根据tan∠EAM=0.62,代入求解即可,于是可得EF=DF+CD,代入求解.
解答 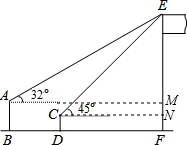 解:过点A作AM⊥EF于点M,过点C作CN⊥EF于点N,
解:过点A作AM⊥EF于点M,过点C作CN⊥EF于点N,
设CN=x,
在Rt△ECN中,
∵∠ECN=45°,
∴EN=CN=x,
∴EM=x+0.7-1.7=x-1,
∵BD=5,
∴AM=BF=5+x,
在Rt△AEM中,
∵∠EAM=32°
∴$\frac{EM}{AM}$=0.62,
∴x-1=0.62(x+5),
解得:x≈10.8,
∴EF=x+0.7≈11.5.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
相关题目
6.在△ABC中,a:b:c=1:1:$\sqrt{2}$,那么△ABC是( )
| A. | 等腰三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
9. 如图,已知AB∥CD,那么下列结论中正确的是( )
如图,已知AB∥CD,那么下列结论中正确的是( )
 如图,已知AB∥CD,那么下列结论中正确的是( )
如图,已知AB∥CD,那么下列结论中正确的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠2=∠3 | D. | ∠1+∠ACD=180° |
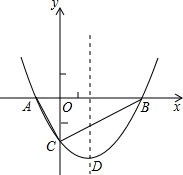 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).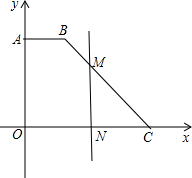 已知A(0,4)、B(2,4)、C(6,0),点M是折线A-B-C上的一个动点,MN⊥x轴于N,设ON的长为x,△MOC的面积是S,写出S与x之间的函数关系式?
已知A(0,4)、B(2,4)、C(6,0),点M是折线A-B-C上的一个动点,MN⊥x轴于N,设ON的长为x,△MOC的面积是S,写出S与x之间的函数关系式?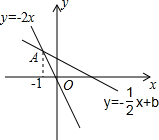 如图,在平面直角坐标系中直线y=-2x与y=-$\frac{1}{2}$x+b交于点A,则关于x,y的方程组$\left\{\begin{array}{l}{x+2y=2b}\\{2x+y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.
如图,在平面直角坐标系中直线y=-2x与y=-$\frac{1}{2}$x+b交于点A,则关于x,y的方程组$\left\{\begin{array}{l}{x+2y=2b}\\{2x+y=0}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$.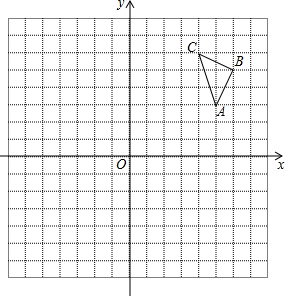 在平面直角坐标系中,△ABC的三个顶点坐标分别为A(5,3),B(6,5),C(4,6).
在平面直角坐标系中,△ABC的三个顶点坐标分别为A(5,3),B(6,5),C(4,6).