题目内容
5.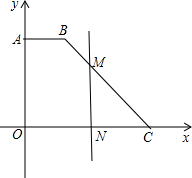 已知A(0,4)、B(2,4)、C(6,0),点M是折线A-B-C上的一个动点,MN⊥x轴于N,设ON的长为x,△MOC的面积是S,写出S与x之间的函数关系式?
已知A(0,4)、B(2,4)、C(6,0),点M是折线A-B-C上的一个动点,MN⊥x轴于N,设ON的长为x,△MOC的面积是S,写出S与x之间的函数关系式?
分析 分两种情形:①当点M在AB上时即0≤x≤2,②当点M在BC上时即2<x≤6,分别求出△MOC的面积即可.
解答 解:①当点M在AB上时即0≤x≤2时,s=$\frac{1}{2}$×6×4=12.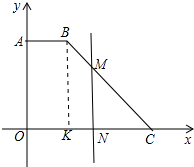
②当点M在BC上时即2<x≤6时,作BK⊥OC于K,
∵A(0,4)、B(2,4)、C(6,0),
∴AB∥OC,
∵BK∥AO,
∴四边形ABKO是平行四边形,
∴∠AOK=90°,
∴四边形ABKO是矩形,
∴AB=OK=2,AO=BK=4,KC=OC-OK=4,
∴BK=KC,∵∠BKC=90°,
∴∠BCK=∠CBK=∠NMC=45°,
∴MN=NC=6-x,
∴s=$\frac{1}{2}$×6×(6-x)=-3x+18.
综上所述y=$\left\{\begin{array}{l}{12}&{(0≤x≤2)}\\{-3x+18}&{(2<x≤6)}\end{array}\right.$.
点评 本题考查动点问题的函数图象、矩形的判定和性质、三角形的面积等知识解题的关键是学会讨论讨论的思想,正确确定自变量的取值范围,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若am=2,an=3,则am+2n等于( )
| A. | 18 | B. | 12 | C. | 11 | D. | 8 |
12.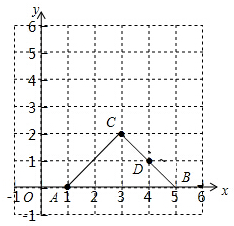 如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
①(2,1)②(3,1)③(4,2)④(5,2)
 如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )①(2,1)②(3,1)③(4,2)④(5,2)
| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
10.在平面直角坐标系中,已知点A(2,m)和点B(n,-3)关于x轴对称,则m+n的值是( )
| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
17.下列图形中,既是中心对称图形又是轴对称图形的有( )个.
①线段;②等边三角形;③矩形;④菱形;⑤五角星;⑥圆.
①线段;②等边三角形;③矩形;④菱形;⑤五角星;⑥圆.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
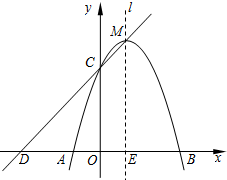 如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2+2x+c与x轴交于点A(-1,0)和点B,与y轴相交于点C(0,3),抛物线的对称轴为直线l.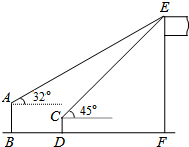 如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)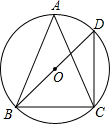 如图,⊙O是△ABC的外接圆,∠A=45°,BD为⊙O的直径,BD=$\sqrt{2}$,连结CD,则CD的长为1.
如图,⊙O是△ABC的外接圆,∠A=45°,BD为⊙O的直径,BD=$\sqrt{2}$,连结CD,则CD的长为1.