题目内容
11.已知在平面直角坐标系中,点A(-1,0)和C(1,1),动点D(t,t)(点D与点C不重合),二次函数y=ax2-4ax+c的图象与x轴相交于点A和B.(1)设二次函数y=ax2-4ax+c的顶点为P,若点P与点D关于x轴对称,求此二次函数的解析式.
(2)在D运动时,若在坐标轴上找一点Q,使△QCD为直角三角形,这样的点Q有且仅有4个,求满足条件的t的值或取值范围.
分析 (1)可先求出点P的横坐标,从而可求出点D的坐标,然后把点A、D的坐标代入抛物线的解析式,就可解决问题;
(2)只需先考虑几个临界位置(①点D在原点,②点D在线段OC上,且以CD为直径的圆与坐标轴相切,③点D在线段OC的延长线上,且以CD为直径的圆与坐标轴相切),然后结合图象就可解决问题.
解答 解:(1)由题意得:点P的横坐标为-$\frac{-4a}{2a}$=2.
∵点P与点D关于x轴对称,
∴点D的横坐标为2,
∴t=2,
∴点D(2,2).
把点A(-1,0),D(2,2)代入y=ax2-4ax+c得:$\left\{\begin{array}{l}{a+4a+c=0}\\{4a-8a+c=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{2}{9}}\\{c=-\frac{10}{9}}\end{array}\right.$,
∴二次函数的解析式为y=$\frac{2}{9}$x2-$\frac{8}{9}$x-$\frac{10}{9}$;
(2)①当点D在原点时,
以点C为直角顶点的点Q有两个,
以点D为直角顶点的点Q不存在,
以点Q为直角顶点的点Q有两个(此时点Q是以CD为直径的圆与坐标轴的交点),
∴当点D在原点时,使△QCD为直角三角形的点Q有且仅有4个,此时t=0;
②当点D在线段OC上,且以CD为直径的⊙E与坐标轴相切时,如图1,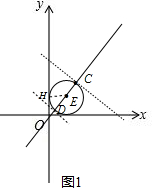
以点C为直角顶点的点Q有两个,
以点D为直角顶点的点Q有两个,
以点Q为直角顶点的点Q有两个(此时点Q是以CD为直径的圆与坐标轴的交点),
∴使△QCD为直角三角形的点Q有且仅有6个,此时点E到坐标轴的距离EH等于⊙E的半径EC,则有
$\frac{\sqrt{2}(1-t)}{2}$=$\frac{t+1}{2}$,
解得t=3-2$\sqrt{2}$;
③当点D在线段OC延长线上,且以CD为直径的⊙E与坐标轴相切时,如图2,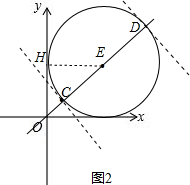
以点C为直角顶点的点Q有两个,
以点D为直角顶点的点Q有两个,
以点Q为直角顶点的点Q有两个(此时点Q是以CD为直径的圆与坐标轴的交点),
∴使△QCD为直角三角形的点Q有且仅有6个,此时点E到坐标轴的距离EH等于⊙E的半径EC,则有
$\frac{\sqrt{2}(t-1)}{2}$=$\frac{t+1}{2}$,
解得t=3+2$\sqrt{2}$.
结合图象可得:满足条件的t的取值范围是3-2$\sqrt{2}$<t<3+2$\sqrt{2}$或t=0.
点评 本题主要考查了运用待定系数法求抛物线的解析式、抛物线的对称轴、两点关于x轴对称、直线与圆相切、圆周角定理等知识,运用分类讨论的思想和临界值法是解决第(2)小题的关键.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )
如图,AB是⊙O的直径,弦CA=CB,D是AMB上一动点与A、B点不重合),则∠D的度数是( )| A. | 30° | B. | 40° | C. | 45° | D. | 60° |
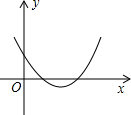 已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,b2-4ac>0.
已知二次函数y=ax2+bx+c的图象如图所示,则a>0,b<0,c>0,b2-4ac>0.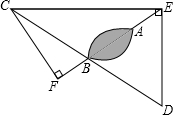 海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=$\frac{3}{5}$.
海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=$\frac{3}{5}$.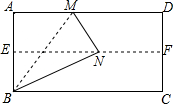 如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):
如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):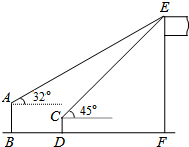 如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)