题目内容
7.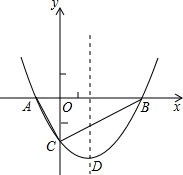 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
分析 (1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据勾股定理的逆定理,可得答案;
(3)根据轴对称的性质,两点之间线段最短,可得M点是对称轴与BC的交点,根据自变量与函数值的对应关系,可得答案.
解答 解:(1)∵点A(-1,0)在抛物线y=x2+bx-2上,
∴$\frac{1}{2}$×(-1)2+b×(-1)-2=0,
解得 b=-$\frac{3}{2}$,
∴抛物线的解析式为y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2.
∵y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2=$\frac{1}{2}$(x-$\frac{3}{2}$)2-$\frac{25}{8}$,
∴顶点D的坐标为($\frac{3}{2}$,-$\frac{25}{8}$);
(2)△ABC是直角三角形.理由如下:
当x=0时,y=-2,
∴C(0,-2),则OC=2.
当y=0时,$\frac{1}{2}$x2-$\frac{3}{2}$x-2=0,
∴x1=-1,x2=4,则B(4,0),
∴OA=1,OB=4,
∴AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(3)由题意A、B两点关于对称轴对称,故直线BC与对称轴的交点即为点M.
由B(4,0),C(0,-2)
设直线BC:y=kx-2
4k-2=0,
k=$\frac{1}{2}$.
所以直线BC:y=$\frac{1}{2}$x-2.
当x=$\frac{3}{2}$时,y=$\frac{1}{2}$×$\frac{3}{2}$-2=-$\frac{5}{4}$.
所以M($\frac{3}{2}$,-$\frac{5}{4}$).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用勾股定理的逆定理判定三角形的形状;利用轴对称的性质得出M是BC与对称轴的交点是解题关键.

| A. | 东北方向 | B. | 东经35°10′,北纬12° | ||
| C. | 距点A100米 | D. | 偏北20°,10000米 |
| A. | a>0 | B. | a>2 | C. | a<0 | D. | a<2 |
 如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )
如图,已知长方体的长宽高分别为4、2、1,一只蚂蚁沿长方体的表面,从点A爬到点B,最短路程为( )| A. | $\sqrt{29}$ | B. | $\sqrt{37}$ | C. | $\sqrt{21}$ | D. | 5 |
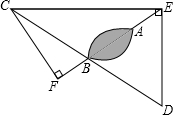 海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=$\frac{3}{5}$.
海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=$\frac{3}{5}$.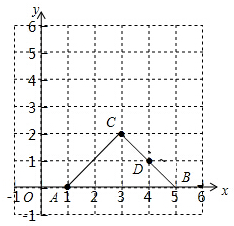 如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )
如图,点A、B、C、D的坐标分别是(1,0)、(5,0)、(3,2)、(4,1),如果以点C、D、E为顶点的直角三角形与△ABC相似,则E点的坐标可能是下列的( )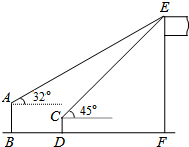 如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
如图,一个数学兴趣小组在活动课上测得学校旗杆的高度,已知小明站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为32°小红蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果精确度0.1米,参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)