题目内容
20.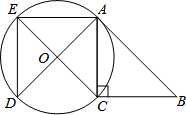 如图,在△ABC中,∠ACB=90°,△ADE是由△ABC绕点A顺时针旋转得到的,以CE为直径的⊙O恰好经过点A、D,求证:AB是⊙O的切线.
如图,在△ABC中,∠ACB=90°,△ADE是由△ABC绕点A顺时针旋转得到的,以CE为直径的⊙O恰好经过点A、D,求证:AB是⊙O的切线.
分析 欲证明AB是⊙O的切线,只需推知AD⊥AB即可.
解答 证明:∵△ADE是由△ABC绕点A顺时针旋转得到的,
∴∠EAD=∠CAB.
∵CE是直径,
∴∠EAC=90°即∠EAD+∠DAC=90°.
∵∠EAD=∠CAB,
∴∠CAB+∠DAC=90°即∠DAB=90°,
∴AD⊥AB.
∵∠AED=90°,
∴AD是直径.
又∵AD⊥AB,
∴AB是⊙O的切线.
点评 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
10.已知方程组$\left\{\begin{array}{l}{a+2b=4}\\{3a+2b=8}\end{array}\right.$,则点(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.下列各组的两项不是同类项的是( )
| A. | 2ax2与3x2 | B. | -1和3 | C. | 2xy2和-y2x | D. | 8xy和-8xy |
15.正三角形ABC的内切圆半径为1,则△ABC的边长是( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |