题目内容
10.阅读:$\frac{2}{\sqrt{3}+1}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{2}$=$\sqrt{3}$-1(此方法常用)
或:$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{(\sqrt{3})^2-1^2}{\sqrt{3}+1}$=$\frac{(\sqrt{3}+1)(\sqrt{3}-1)}{\sqrt{3}+1}$=$\sqrt{3}$-1
化简:
①$\frac{1}{\sqrt{5}+\sqrt{2}}$=$\frac{\sqrt{5}-\sqrt{2}}{3}$;
②$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2n+1}+\sqrt{2n-1}}$.
分析 ①根据二次根式的乘除法法则进行二次根式有理化,可得答案;
②根据分母有理化,可得二次根式的加减,根据二次根式的加减,可得答案.
解答 解:①原式=$\frac{\sqrt{5}-\sqrt{2}}{(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})}$=$\frac{\sqrt{5}-\sqrt{2}}{3}$,
故答案为:$\frac{\sqrt{5}-\sqrt{2}}{3}$;
②原式=$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{5}-\sqrt{3}}{2}$+$\frac{\sqrt{7}-\sqrt{5}}{2}$+…+$\frac{\sqrt{2n+1}-\sqrt{2n-1}}{2}$
=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$…+$\sqrt{2n+1}$-$\sqrt{2n-1}$)
=$\frac{1}{2}$($\sqrt{2n+1}$-1)
=$\frac{\sqrt{2n+1}-1}{2}$.
点评 主要考查二次根式的有理化.利用二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.当x=( )时,|x+6|有最( )值,是( )
| A. | 0,大,0 | B. | 0,小,0 | C. | -6,大,0 | D. | -6,小,0 |
17.在-8,2.6,-3$\frac{1}{2}$,2$\frac{2}{3}$,-5.7中,负分数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
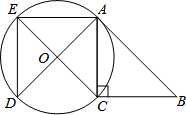 如图,在△ABC中,∠ACB=90°,△ADE是由△ABC绕点A顺时针旋转得到的,以CE为直径的⊙O恰好经过点A、D,求证:AB是⊙O的切线.
如图,在△ABC中,∠ACB=90°,△ADE是由△ABC绕点A顺时针旋转得到的,以CE为直径的⊙O恰好经过点A、D,求证:AB是⊙O的切线. 如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.
如图,已知点O在直线AB上,0D、0E分别平分∠BOC、∠AOC,∠BOC=80°.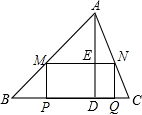 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.