题目内容
15.正三角形ABC的内切圆半径为1,则△ABC的边长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
分析 由切线的性质可知OD⊥BC,由三角形内心的性质可知∠OCD=30°,最后利用特殊锐角三角函数值求解即可.
解答 解;如图所示:连接OC、OD.
∵BC与圆O相切,
∴OD⊥BC.
∵△ABC为正三角形,
∴∠ACB=60°.
∵O是△ABC的内心,
∴∠OCD=$\frac{1}{2}∠ACD$=30°.
∴DC=$\sqrt{3}$OD=$\sqrt{3}×1=\sqrt{3}$.
∴BC=2$\sqrt{3}$.
故选B.
点评 本题主要考查的是三角形的内心,证得△OCD为直角三角三角形且∠OCD=30°是解题的关键.

练习册系列答案
相关题目
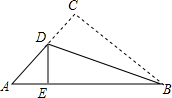 如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD翻折后,若点C恰好落在AB边上的点E处,则△ADE的周长为7.
如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD翻折后,若点C恰好落在AB边上的点E处,则△ADE的周长为7. 如图,在梯形ABCD中,AB∥DC,DE∥CB,△AED的周长为18,EB=4,则梯形ABCD的周长为26.
如图,在梯形ABCD中,AB∥DC,DE∥CB,△AED的周长为18,EB=4,则梯形ABCD的周长为26.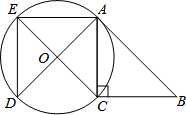 如图,在△ABC中,∠ACB=90°,△ADE是由△ABC绕点A顺时针旋转得到的,以CE为直径的⊙O恰好经过点A、D,求证:AB是⊙O的切线.
如图,在△ABC中,∠ACB=90°,△ADE是由△ABC绕点A顺时针旋转得到的,以CE为直径的⊙O恰好经过点A、D,求证:AB是⊙O的切线.