题目内容
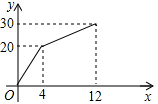 一个装有进、出水管的容器,单位时间内进、出水量都是常量,没开始的4min内只进水不出水,在随后的8min内既进水又出水,得到时间x(min)与水量y(L)的函数图象(如图).
一个装有进、出水管的容器,单位时间内进、出水量都是常量,没开始的4min内只进水不出水,在随后的8min内既进水又出水,得到时间x(min)与水量y(L)的函数图象(如图).(1)每分钟进水多少?
(2)当4≤x≤12时,写出y与x之间的函数表达式;
(3)当12min后只放水不进水,求y与x之间的函数表达式.
考点:一次函数的应用
专题:
分析:(1)由函数图象,根据工作效率=工作总量÷工作时间就可以得出结论;
(2)当4≤x≤12时,设y与x之间的函数表达式为y=kx+b,由待定系数法求出其值即可;
(3)由(2)求出水管每分钟的工作效率,就可以求出12分钟后只放水不进水的时间,12min后只放水不进水,设y与x之间的函数表达式为y=k1x+b1,由待定系数法求出其解即可.
(2)当4≤x≤12时,设y与x之间的函数表达式为y=kx+b,由待定系数法求出其值即可;
(3)由(2)求出水管每分钟的工作效率,就可以求出12分钟后只放水不进水的时间,12min后只放水不进水,设y与x之间的函数表达式为y=k1x+b1,由待定系数法求出其解即可.
解答:解:(1)由函数图象,得
20÷4=5L.
答:每分钟进水5L;
(2)当4≤x≤12时,设y与x之间的函数表达式为y=kx+b,由题意,得
,
解得:
,
∴y=1.25x+15.
答:y与x之间的函数表达式为:y=1.25x+15;
(3)由图象,得
放水的效率为:5-(30-20)÷8=3.75,
∴当12min后只放水不进水需要的时间为:30÷3.75=8分钟,
∴20分钟时,容器的水放完.
12min后只放水不进水,设y与x之间的函数表达式为y=k1x+b1,由题意,得
,
解得:
,
∴y=-3.75x+75(12≤x≤20).
答:当12min后只放水不进水,y与x之间的函数表达式为y=-3.75x+75(12≤x≤20).
20÷4=5L.
答:每分钟进水5L;
(2)当4≤x≤12时,设y与x之间的函数表达式为y=kx+b,由题意,得
|
解得:
|
∴y=1.25x+15.
答:y与x之间的函数表达式为:y=1.25x+15;
(3)由图象,得
放水的效率为:5-(30-20)÷8=3.75,
∴当12min后只放水不进水需要的时间为:30÷3.75=8分钟,
∴20分钟时,容器的水放完.
12min后只放水不进水,设y与x之间的函数表达式为y=k1x+b1,由题意,得
|
解得:
|
∴y=-3.75x+75(12≤x≤20).
答:当12min后只放水不进水,y与x之间的函数表达式为y=-3.75x+75(12≤x≤20).
点评:本题考查了工程问题的数量关系工作效率=工作总量÷工作时间的运用,待定系数法求一次函数的解析式的运用,解答时求出函数的解析式是关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
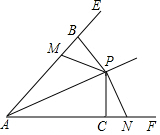 如图所示,已知∠EAF,FB⊥AE于点B,PC⊥AF于点C,M,N分别是射线AE,AF上的点,∠PNC=∠PMB,PM=PN.求证:AP平分∠EAF.
如图所示,已知∠EAF,FB⊥AE于点B,PC⊥AF于点C,M,N分别是射线AE,AF上的点,∠PNC=∠PMB,PM=PN.求证:AP平分∠EAF. 如图,直线AB、CD相交于点O,∠1=35°,∠2=75°,求∠EOB的度数.
如图,直线AB、CD相交于点O,∠1=35°,∠2=75°,求∠EOB的度数. 已知,AB=AD,CB=CD.
已知,AB=AD,CB=CD.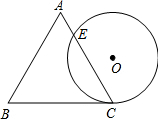 一个边长为2cm的等边△ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为
一个边长为2cm的等边△ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为
 用适当语句表述图中点与直线的关系:
用适当语句表述图中点与直线的关系: