题目内容
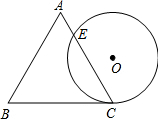 一个边长为2cm的等边△ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为
一个边长为2cm的等边△ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为考点:切线的性质,等边三角形的性质
专题:
分析:连接OC,并过点O作OF⊥CE于F,根据等边三角形的性质,等边三角形的高等于底边的
倍.已知边长为2cm的等边三角形ABC与⊙O等高,说明⊙O的半径为
,即OC=
,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
解答: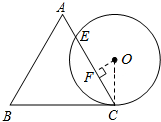 解:连接OC,过点O作OF⊥CE于F,
解:连接OC,过点O作OF⊥CE于F,
∵△ABC为等边三角形,边长为2,
∴△ABC的高为
,即OC=
,
∵⊙O与BC相切于点C,
∴OC⊥BC,
又∵∠ACB=60°,
∴∠OCF=30°,
在Rt△OFC中,FC=OC•cos30°=
×
=
,
∵OF过圆心,且OF⊥CE,
∴CE=2FC=
cm.
故答案为:
.
 解:连接OC,过点O作OF⊥CE于F,
解:连接OC,过点O作OF⊥CE于F,∵△ABC为等边三角形,边长为2,
∴△ABC的高为
| 3 |
| ||
| 2 |
∵⊙O与BC相切于点C,
∴OC⊥BC,
又∵∠ACB=60°,
∴∠OCF=30°,
在Rt△OFC中,FC=OC•cos30°=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
∵OF过圆心,且OF⊥CE,
∴CE=2FC=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题主要考查了切线的性质和等边三角形的性质和解直角三角形的有关知识.题目不是太难,属于基础性题目.

练习册系列答案
相关题目
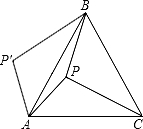 如图,P是正△ABC内的一点,若将△PAC绕点A逆时针旋转到△P′AB,
如图,P是正△ABC内的一点,若将△PAC绕点A逆时针旋转到△P′AB,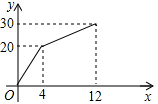 一个装有进、出水管的容器,单位时间内进、出水量都是常量,没开始的4min内只进水不出水,在随后的8min内既进水又出水,得到时间x(min)与水量y(L)的函数图象(如图).
一个装有进、出水管的容器,单位时间内进、出水量都是常量,没开始的4min内只进水不出水,在随后的8min内既进水又出水,得到时间x(min)与水量y(L)的函数图象(如图). 请把下列各数在数轴上表示出来,然后用“<”连接.
请把下列各数在数轴上表示出来,然后用“<”连接.