题目内容
在△ABC中，∠A=30°，sinB=
，AC=2
，则AB= ．
| ||
| 2 |
| 3 |
考点：解直角三角形
专题：
分析：根据特殊角的三角函数值求出∠B，得出直角三角形，解直角三角形求出BA即可．
解答：解：
∵sinB=
，
∴∠B=60°，
∵∠A=30°，
∴∠C=180°-60°-30°=90°，
即△ABC是直角三角形，
∴AB=
=
=4，
故答案为：4．
∵sinB=
| ||
| 2 |
∴∠B=60°，
∵∠A=30°，
∴∠C=180°-60°-30°=90°，
即△ABC是直角三角形，
∴AB=
| AC |
| sinB |
2
| ||
| sin60° |
故答案为：4．
点评：本题考查了特殊角的三角函数值，解直角三角形的应用，解此题的关键是求出∠B的度数和得出直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
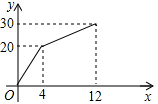一个装有进、出水管的容器，单位时间内进、出水量都是常量，没开始的4min内只进水不出水，在随后的8min内既进水又出水，得到时间x（min）与水量y（L）的函数图象（如图）．
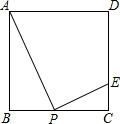已知ABCD是正方形，E是CD上一点，且