题目内容
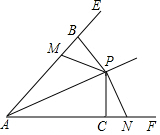 如图所示,已知∠EAF,FB⊥AE于点B,PC⊥AF于点C,M,N分别是射线AE,AF上的点,∠PNC=∠PMB,PM=PN.求证:AP平分∠EAF.
如图所示,已知∠EAF,FB⊥AE于点B,PC⊥AF于点C,M,N分别是射线AE,AF上的点,∠PNC=∠PMB,PM=PN.求证:AP平分∠EAF.考点:角平分线的性质
专题:证明题
分析:利用条件证明△PBM≌△PCN,可得到PB=PC,由角平分线的判定可得出结论.
解答:证明:
∵PB⊥AE,PC⊥AF,
∴∠PBM=∠PCN,
在△PBM和△PCN中
∴△PBM≌△PCN(AAS),
∴PB=PC,
∴点P在∠EAF的平分线上,
即AP平分∠EAF.
∵PB⊥AE,PC⊥AF,
∴∠PBM=∠PCN,
在△PBM和△PCN中
|
∴△PBM≌△PCN(AAS),
∴PB=PC,
∴点P在∠EAF的平分线上,
即AP平分∠EAF.
点评:本题主要考查角平分线的判定,掌握到角两边距离相等的点在角的平分线上是解题的关键.

练习册系列答案
相关题目
已知一元二次方程x2-6x+c=0有一根为2,则另一根为( )
| A、3 | B、-3 | C、4 | D、-4 |
 如图,AB⊥BC,CD⊥BC,AB=2,CD=3,BC=7,M为BC上一点,当M为何值时△ABM和△CDM相似?
如图,AB⊥BC,CD⊥BC,AB=2,CD=3,BC=7,M为BC上一点,当M为何值时△ABM和△CDM相似?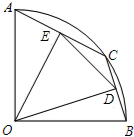 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是
如图,在半径为5的扇形AOB中,∠AOB=90°,点C是
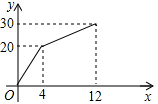 一个装有进、出水管的容器,单位时间内进、出水量都是常量,没开始的4min内只进水不出水,在随后的8min内既进水又出水,得到时间x(min)与水量y(L)的函数图象(如图).
一个装有进、出水管的容器,单位时间内进、出水量都是常量,没开始的4min内只进水不出水,在随后的8min内既进水又出水,得到时间x(min)与水量y(L)的函数图象(如图).