题目内容
我们知道：有理数和数轴上的点之间有对应关系，这揭示了数与点之间的内在联系，它是“数形结合”的基础．
（1）在数轴上表示-2和4两点之间的距离是 ；
（2）在纸上画出一条数轴，分别按下列方式折叠这张纸；
①若-2和4表示的两点重合，则2表示的点与数 表示的点重合；
②若-5和3表示的两点重合，则-3表示的点和数 表示的点重合；这时如果A、B两点之间的距离为2012，且A、B两点经折叠后重合，则点A表示的数是 ．
（1）在数轴上表示-2和4两点之间的距离是
（2）在纸上画出一条数轴，分别按下列方式折叠这张纸；
①若-2和4表示的两点重合，则2表示的点与数
②若-5和3表示的两点重合，则-3表示的点和数
考点：数轴
专题：
分析：（1）列出算式4-（-2），求出即可；
（2）①根据折叠-2和4重合，即可得出答案．
②根据折叠-5和3重合，即可得出-3和1重合，当A是-1007时B是1005，当A是1005时B是-1007，两种情况都符合．
（2）①根据折叠-2和4重合，即可得出答案．
②根据折叠-5和3重合，即可得出-3和1重合，当A是-1007时B是1005，当A是1005时B是-1007，两种情况都符合．
解答：解：1）4-（-2）=6．
故在数轴上表示-2和4两点之间的距离是6；
（2）①∵-2和4表示的两点重合，
∴2表示的点与数0表示的点重合；
②∵-5和3表示的两点重合，
∴-3表示的点和数1表示的点重合；
∵A、B两点之间的距离为2012，且A、B两点经折叠后重合，
∴点A表示的数是-1007或1005．
故答案为：6；0；1，-1007或1005．
故在数轴上表示-2和4两点之间的距离是6；
（2）①∵-2和4表示的两点重合，
∴2表示的点与数0表示的点重合；
②∵-5和3表示的两点重合，
∴-3表示的点和数1表示的点重合；
∵A、B两点之间的距离为2012，且A、B两点经折叠后重合，
∴点A表示的数是-1007或1005．
故答案为：6；0；1，-1007或1005．
点评：本题考查了数轴，折叠的应用，主要考查学生的理解能力和计算能力．
练习册系列答案
相关题目
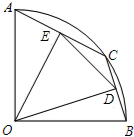如图，在半径为5的扇形AOB中，∠AOB=90°，点C是
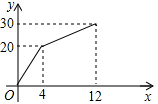一个装有进、出水管的容器，单位时间内进、出水量都是常量，没开始的4min内只进水不出水，在随后的8min内既进水又出水，得到时间x（min）与水量y（L）的函数图象（如图）．
如图，△ABC中，∠ACB=90°，AC=BC=5，BE⊥CE于E，AD⊥CE于D，AD=4，BE=3，则DE=
请把下列各数在数轴上表示出来，然后用“＜”连接．
的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．所以式子|x-3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离．