题目内容
18. 在Rt△ABC中,∠C=90°,D为BC边(除端点外)上的一点,设∠ADC=α,∠B=β,
在Rt△ABC中,∠C=90°,D为BC边(除端点外)上的一点,设∠ADC=α,∠B=β,(1)猜想sinα与sinβ的大小关系;
(2)试证明你的结论.
(3)猜想锐角α、β与它们正弦值的规律.
分析 (1)根据正弦函数定义即可作出判断;
(2)利用三角函数的定义,利用直角三角形的边表示出三角函数,根据三角形的边即可判断;
(3)根据(2)的结论即可解答.
解答 解:(1)sinα>sinβ;
(2)证明:∵sinα=$\frac{AC}{AD}$,sinβ=$\frac{AC}{AB}$,
又∵AD<AB,
∴sinα>sinβ;
(3)当α>β时,sinα>sinβ;
当α=β时,sinα=sinβ;
α<β时,sinα<sinβ.
点评 本题考查了正弦函数的定义,在直角三角形中,锐角的正弦为对边比斜边.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图,BC∥ED,计算AB、AC的长.(使用证明的方法)
如图,BC∥ED,计算AB、AC的长.(使用证明的方法) 读图,完成图后的两个小题:
读图,完成图后的两个小题: 如图所示,已知∠AOB=68°,过点O画射线OC,使∠BOC=31°,并求∠AOC的度数.
如图所示,已知∠AOB=68°,过点O画射线OC,使∠BOC=31°,并求∠AOC的度数. 观察函数y=2x-5的图象,回答下列问题:
观察函数y=2x-5的图象,回答下列问题: 如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.
如图,矩形草坪长30m、宽20m,沿草坪四周有1m宽的环形小路,小路内外边缘形成的两个矩形相似吗?说出你的理由.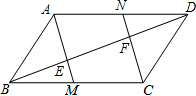 如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.
如图,在平行四边形ABCD中,M、N分别为BC、DA中点,AM、CN分别交BD于点E、F,求证:BE=EF=FD.