题目内容
8.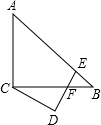 如图,△ABC中,∠ACB=90°,AC=BC,E为AB上一点,∠CDE=90°,且CD=DE,DE交BC于点F.若∠BCD=30°,AB=4$\sqrt{3}$,则DF的长为$\frac{2\sqrt{6}}{3}$.
如图,△ABC中,∠ACB=90°,AC=BC,E为AB上一点,∠CDE=90°,且CD=DE,DE交BC于点F.若∠BCD=30°,AB=4$\sqrt{3}$,则DF的长为$\frac{2\sqrt{6}}{3}$.
分析 由DC=DE,想到构造全等三角形,故作DN⊥AC于N,EH⊥BC垂足为H,ND与EH交于点M,只要证明△CDN≌△DEM得DN=EM,CN=DM,设DF=a,求出相应的线段,列出关于a的方程即可.
解答 解;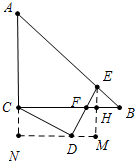 如图作DN⊥AC于N,EH⊥BC垂足为H,ND与EH交于点M.设DF=a.
如图作DN⊥AC于N,EH⊥BC垂足为H,ND与EH交于点M.设DF=a.
∵∠DCF=30°,∠CDF=90°,
∴CD=$\sqrt{3}$a,
在RT△CDN中,∵∠DCN=30°,CD=$\sqrt{3}$a,
∴CN=$\frac{\sqrt{3}}{2}a$,ND=$\frac{3}{2}$a,
∵∠CDN+∠EDM=90°,∠NCD+∠CDN=90°,
∴∠NCD=∠EDM,
在△CDN和△DEM中,
$\left\{\begin{array}{l}{∠NCD=∠EDM}\\{∠CND=∠EMD=90°}\\{CD=ED}\end{array}\right.$,
∴△CDN≌△DEM,
∴DM=CN=$\frac{\sqrt{3}}{2}a$,EM=ND=$\frac{3}{2}$a,
∵∠N=∠NCH=∠M=90°,
∴四边形CNMH是矩形,
∴MH=CN=$\frac{\sqrt{3}}{2}$a,CH=MN$\frac{3}{2}a+\frac{\sqrt{3}}{2}a$,
∵BC=AC,∠ACB=90°,AB=4$\sqrt{3}$
∴∠B=45°,BC=2$\sqrt{6}$,
∴∠HEB=∠B=45°,
∴EH=HB=EM-HM=$\frac{3}{2}a-\frac{\sqrt{3}}{2}a$,
∴$\frac{3}{2}a$+$\frac{\sqrt{3}}{2}a$+$\frac{3}{2}a$-$\frac{\sqrt{3}}{2}$a=2$\sqrt{6}$,
∴a=$\frac{2\sqrt{6}}{3}$.
故答案为$\frac{2\sqrt{6}}{3}$.
点评 本题考查勾股定理、等腰直角三角形的性质、全等三角形的判定和性质、矩形的性质等知识,解题的关键是添加辅助线构造全等三角形,属于中考填空题的压轴题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案| A. | a3•a3=a9 | B. | (a3)2=a5 | C. | (2ab2)3=6a3b6 | D. | (-a)7÷(-a)2=-a5 |
 如图.在四边形ABCD中,AB∥CD,∠B=∠D,AE平分∠BAD交BC于E.若AB=2,AE=2$\sqrt{2}$,试判断四边形ABCD的形状,并说明理由.
如图.在四边形ABCD中,AB∥CD,∠B=∠D,AE平分∠BAD交BC于E.若AB=2,AE=2$\sqrt{2}$,试判断四边形ABCD的形状,并说明理由.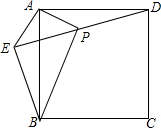 如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论:
如图,在正方形ABCD外取一点E,连接AE,BE,DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=$\sqrt{6}$,下列结论: