题目内容
13. 如图.在四边形ABCD中,AB∥CD,∠B=∠D,AE平分∠BAD交BC于E.若AB=2,AE=2$\sqrt{2}$,试判断四边形ABCD的形状,并说明理由.
如图.在四边形ABCD中,AB∥CD,∠B=∠D,AE平分∠BAD交BC于E.若AB=2,AE=2$\sqrt{2}$,试判断四边形ABCD的形状,并说明理由.
分析 由平行线的性质和已知条件得出∠D+∠C=180°,证出AD∥BC,得出四边形ABCD是平行四边形,由平行线的性质和已知条件得出∠BAE=∠AEB,证出BE=AB=2,由勾股定理的逆定理证出△ABE是直角三角形,∠B=90°,即可得出四边形ABCD是矩形.
解答 解:四边形ABCD是矩形;理由如下:
∵AB∥CD,
∴∠B+∠C=180°,
∵∠B=∠D,
∴∠D+∠C=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=2,
∵AB2+BE2=22+22=8=(2$\sqrt{2}$)2=AE2,
∴△ABE是直角三角形,∠B=90°,
∴四边形ABCD是矩形.
点评 本题考查了平行四边形的判定、平行线的性质、矩形的判定、勾股定理的逆定理;熟练掌握矩形的判定方法,由勾股定理的逆定理证出∠B=90°是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
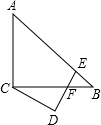 如图,△ABC中,∠ACB=90°,AC=BC,E为AB上一点,∠CDE=90°,且CD=DE,DE交BC于点F.若∠BCD=30°,AB=4$\sqrt{3}$,则DF的长为$\frac{2\sqrt{6}}{3}$.
如图,△ABC中,∠ACB=90°,AC=BC,E为AB上一点,∠CDE=90°,且CD=DE,DE交BC于点F.若∠BCD=30°,AB=4$\sqrt{3}$,则DF的长为$\frac{2\sqrt{6}}{3}$.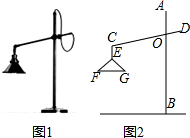 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.