题目内容
20.因式分解:(1)16x4-1;
(2)(x+m)2-(x+n)2;
(3)(x-4)(x+1)+3x.
分析 (1)根据平方差公式a2-b2=(a+b)(a-b)计算即可;
(2)根据平方差公式a2-b2=(a+b)(a-b)计算即可;
(3)先去括号,再运用公式进行分解即可.
解答 解:(1)原式=(4x2+1)(4x2-1)
=(4x2+1)(2x+1)(2x-1);
(2)原式=[(x+m)+(x+n)][(x+m)-(x+n)]
=(2x+m+n)(m-n);
(3)原式=x2-3x-4+3x
=(x+2)(x-2).
点评 本题考查了因式分解-运用公式,熟练掌握平方差公式a2-b2=(a+b)(a-b)是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.若方程组$\left\{\begin{array}{l}{1998x+2006y=2007}\\{(|a|-2)z+5x=5}\end{array}\right.$是二元一次方程组,则a等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
6.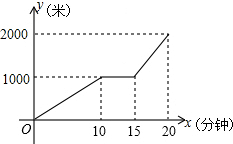 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
 某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )
某天小明骑自行车从家出发去学校上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校,设小明出发后所用时间为x(分钟),离家的距离为y(米),y与x的函数的大致图象如图所示,下列说法错误的是( )| A. | 家到学校的距离是2000米 | |
| B. | 修车耽误的时间是5分钟 | |
| C. | 修车后自行车的速度是每分钟200米 | |
| D. | 修车前比修车后速度快 |
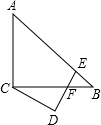 如图,△ABC中,∠ACB=90°,AC=BC,E为AB上一点,∠CDE=90°,且CD=DE,DE交BC于点F.若∠BCD=30°,AB=4$\sqrt{3}$,则DF的长为$\frac{2\sqrt{6}}{3}$.
如图,△ABC中,∠ACB=90°,AC=BC,E为AB上一点,∠CDE=90°,且CD=DE,DE交BC于点F.若∠BCD=30°,AB=4$\sqrt{3}$,则DF的长为$\frac{2\sqrt{6}}{3}$.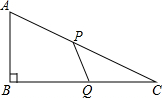 如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止.设移动的时间为t秒.
如图,在△ABC中,∠B=90°,AB=6米,BC=8米,动点P以2米/秒的速度从A点出发,沿AC向点C移动.同时,动点Q以1米/秒的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止.设移动的时间为t秒.