题目内容
3．已知直角三角形的周长为2+$\sqrt{5}$，斜边长为2，求它的面积．分析 根据周长公式可得出a+b=$\sqrt{5}$，结合勾股定理a2+b2=4可得出2ab=1，由三角形的面积公式可知直角三角形的面积为$\frac{1}{2}$ab，从而得出结论．
解答 解：设三角形的两条直角边的长度为a，b．
根据题意可知：$\left\{\begin{array}{l}{a+b+2=2+\sqrt{5}①}\\{{a}^{2}+{b}^{2}={2}^{2}②}\end{array}\right.$，
由①可知：a+b=$\sqrt{5}$③，
③式的平方-②式得：2ab=1，
直角三角形的面积为$\frac{1}{2}$ab=$\frac{1}{4}$．
答：直角三角形的面积为$\frac{1}{4}$．
点评 本题考查了三角形的周长和面积公式，解题的关键是利用a+b=$\sqrt{5}$的平方去减a2+b2=4．本题属于基础题，难度不大，但如果去解方程组，会造成很大的干扰，解决本题巧妙的用到了完全平方公式展开式减去平方和剩下部分为三角形面积的整数倍．
练习册系列答案
相关题目
13．纳米是一种长度单位，1纳米=10-9米，已知某种植物花粉的直径约为15000纳米，那么用科学记数法表示该种花粉的直径为（ ）
| A． | 1.5×10-13米 | B． | 15×10-6米 | C． | 1.5×10-5米 | D． | 1.5×10-6米 |
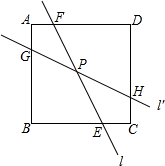如图，直线l经过正方形ABCD内一点P，并交边BC、DA于E、F两点，将直线l绕点P按逆时针方向旋转45°得到直线l′，并交边AB、CD于G、H两点．若AB=4，GH=2$\sqrt{5}$，则EF的值为$\frac{4\sqrt{10}}{3}$．
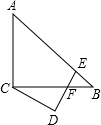如图，△ABC中，∠ACB=90°，AC=BC，E为AB上一点，∠CDE=90°，且CD=DE，DE交BC于点F．若∠BCD=30°，AB=4$\sqrt{3}$，则DF的长为$\frac{2\sqrt{6}}{3}$．