题目内容
11.如图,在△ABC中,∠ACB=90°,AC=BC=$\sqrt{2}$,以点B为圆心,以1为半径作圆.设点P为圆B上一点.线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB.(1)若DP与圆O相切,则∠CPB的度数为45°或135°°;
(2)BD的最小值为1,此时tan∠CBP=1;
(3)BD的最大值为3,此时tan∠CBP=-1.
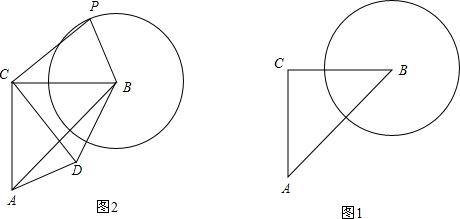
分析 (1)利用切线的性质结合等腰直角三角形得出即可;
(2)当B、D、A三点在同一条直线上时,BD有最小值,此时∠PBC=45°时,BD的最小值为1,此时tan∠CBP=1;
(3)同理可得:如图4,当B、D、A三点在同一条直线上时,BD的最大值为:AB+AD=AB+BP=3,此时tan∠CBP=tan135°=-1.
解答 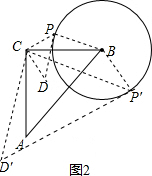 解:(1)如图2,∵CP=CD,DP是⊙B的切线,∠PCD=90°,
解:(1)如图2,∵CP=CD,DP是⊙B的切线,∠PCD=90°,
∴∠BPD=90°,∠ADP=∠APD=45°,
∴∠CPB=45°+90°=135°,
同理可得:∠CPB=45°
故∠CPB=45°或135°;
故答案为:故∠CPB=45°或135°;
(2)如图3,当B、D、A三点在同一条直线上时,BD有最小值,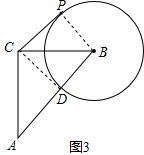 ∵∠ACB=90°,∠DCP=90°,
∵∠ACB=90°,∠DCP=90°,
∴∠ACD=∠BCP
在△ACD与△BCP中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCP}\\{CD=CP}\end{array}\right.$,
∴△ACD≌△BCP(SAS),
∴∠PBC=∠A=45°,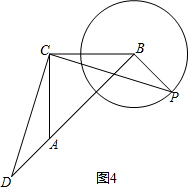 此时∠PBC=45°时,BD的最小值为1,此时tan∠CBP=1;
此时∠PBC=45°时,BD的最小值为1,此时tan∠CBP=1;
(3)同理可得:如图4,当B、D、A三点在同一条直线上时,
BD的最大值为:AB+AD=AB+BP=3,
此时tan∠CBP=tan135°=-1.
故答案为:1,1,3,-1.
点评 此题考查了圆的综合题,涉及的知识有全等三角形的判定与性质,分类思想的运用,最大值与最小值,注意分析问题要全面,以免漏解,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.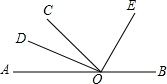 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
 ∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.
∠AOC与∠BOC是邻补角,OD、OE分别是∠AOC与∠BOC的平分线,试判断OD与OE的夹角为( )度.| A. | 60° | B. | 65° | C. | 90° | D. | 80° |
6.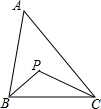 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
 如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )
如图,在△ABC中,∠BAC=40°,点P是△ABC的内心,则∠BPC=( )| A. | 80 | B. | 110 | C. | 130 | D. | 140 |
16.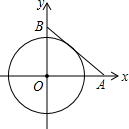 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
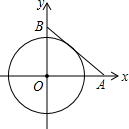 如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )
如图,长为10的线段AB的端点分别在x轴,y轴的正半轴上滑动(线段AB的长保持不变),⊙O与线段AB相切,则⊙O面积的最大值是( )| A. | 100π | B. | 25π | C. | 22π | D. | 20π |
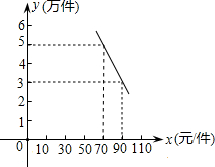 某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系,每年销售该产品的总开支z(万元)(不含进价成本)与年销售y(万件)存在函数关系z=10y+42.5.
某环保器材公司销售一种新型产品,已知每件产品的进价为40元,经销过程中测出销售量y(万件)与销售单价x(元/件)存在如图所示的一次函数关系,每年销售该产品的总开支z(万元)(不含进价成本)与年销售y(万件)存在函数关系z=10y+42.5.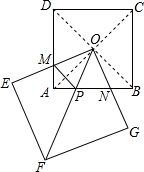 如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
如图,正方形OEFG绕着边长为30的正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.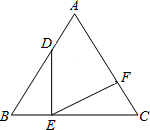 如图,△ABC为等边三角形,点D、E、F分别在AB、BC、CA上,AD=BE,∠DEF=60°,说明AD=CF.
如图,△ABC为等边三角形,点D、E、F分别在AB、BC、CA上,AD=BE,∠DEF=60°,说明AD=CF.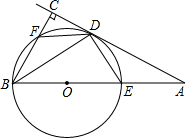 如图,BE是⊙O的直径,A是BE延长线上一点,过A点作⊙O的一条切线,切点为D,过B点作BC⊥AD于C,交⊙O于点F,连接BD.
如图,BE是⊙O的直径,A是BE延长线上一点,过A点作⊙O的一条切线,切点为D,过B点作BC⊥AD于C,交⊙O于点F,连接BD.